How to Find the Width of a Rectangle

Using Area and Length

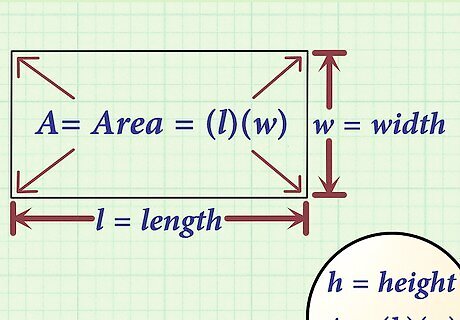
Set up the formula for area of a rectangle. The formula is A = ( l ) ( w ) {\displaystyle A=(l)(w)} A=(l)(w), where A {\displaystyle A} A equals the area of the rectangle, l {\displaystyle l} l equals the length of the rectangle, and w {\displaystyle w} w equals the width of the rectangle. This method will only work if you are given the area and length of the rectangle. You might also see the formula written as A = ( h ) ( w ) {\displaystyle A=(h)(w)} A=(h)(w), where h {\displaystyle h} h equals the height of the rectangle and is used instead of length. These two terms refer to the same measurement.

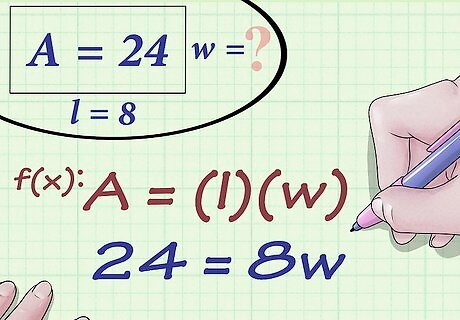
Plug the values for area and length into the formula. Make sure you substitute for the correct variables. For example, if you are trying to find the width of a rectangle that has an area of 24 square centimeters, and a length of 8 centimeters, your formula will look like this: 24 = 8 w {\displaystyle 24=8w} 24=8w

Solve for w {\displaystyle w} w. To do this, you need to divide each side of the equation by the length. For example, in the equation 24 = 8 w {\displaystyle 24=8w} 24=8w, you would divide each side by 8. 24 = 8 w {\displaystyle 24=8w} 24=8w 24 8 = 8 w 8 {\displaystyle {\frac {24}{8}}={\frac {8w}{8}}} {\frac {24}{8}}={\frac {8w}{8}} 3 = w {\displaystyle 3=w} 3=w

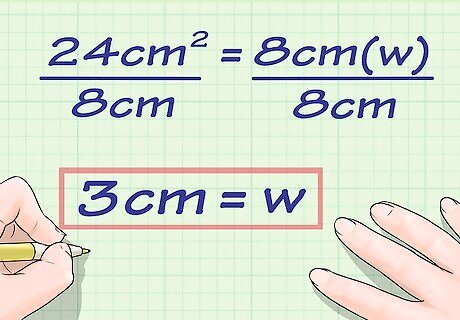
Write your final answer. Don’t forget to include the unit of measurement. For example, for a rectangle with an area of 24 c m 2 {\displaystyle 24cm^{2}} 24cm^{{2}} and a length of 8 c m {\displaystyle 8cm} 8cm, the width would be 3 c m {\displaystyle 3cm} 3cm.

Using Perimeter and Length

Set up the formula for perimeter of a rectangle. The formula is P = 2 l + 2 w {\displaystyle P=2l+2w} P=2l+2w, where P {\displaystyle P} P equals the perimeter of the rectangle, l {\displaystyle l} l equals the length of the rectangle, and w {\displaystyle w} w equals the width of the rectangle. This method will only work if you are given the perimeter and length of the rectangle. You might also see the formula written as P = 2 ( w + h ) {\displaystyle P=2(w+h)} P=2(w+h), where h {\displaystyle h} h equals the height of the rectangle and is used instead of length. The variables l {\displaystyle l} l and h {\displaystyle h} h refer to the same measurement, and the distributive property dictates that these two formulas, although arranged differently, will give you the same result.

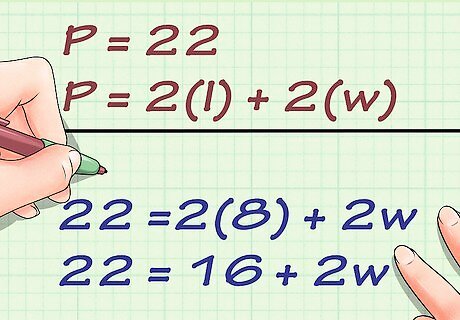
Plug the values for perimeter and length into the formula. Make sure you substitute for the correct variables. For example, if you are trying to find the width of a rectangle that has a perimeter of 22 centimeters, and a length of 8 centimeters, your formula will look like this: 22 = 2 ( 8 ) + 2 w {\displaystyle 22=2(8)+2w} 22=2(8)+2w 22 = 16 + 2 w {\displaystyle 22=16+2w} 22=16+2w

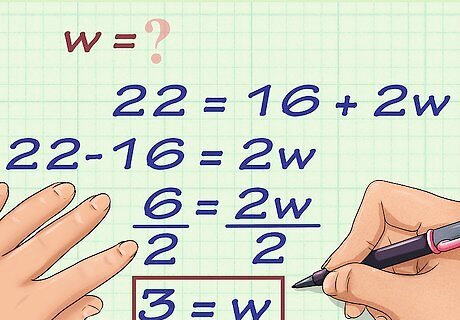
Solve for w {\displaystyle w} w. To do this, you need to subtract the length from each side of the equation, then divide by 2. For example, in the equation 22 = 16 + 2 w {\displaystyle 22=16+2w} 22=16+2w, you would subtract 16 from each side, then divide by 2. 22 = 16 + 2 w {\displaystyle 22=16+2w} 22=16+2w 6 = 2 w {\displaystyle 6=2w} 6=2w 6 2 = 2 w 2 {\displaystyle {\frac {6}{2}}={\frac {2w}{2}}} {\frac {6}{2}}={\frac {2w}{2}} 3 = w {\displaystyle 3=w} 3=w

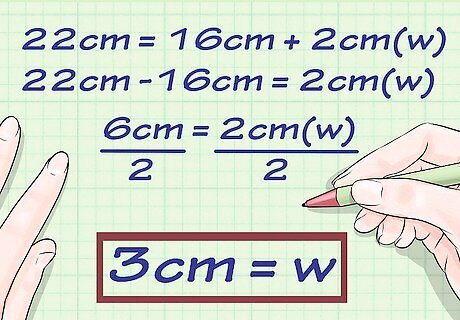
Write your final answer. Don’t forget to include the unit of measurement. For example, for a rectangle with a perimeter of 22 c m {\displaystyle 22cm} 22cm and a length of 8 c m {\displaystyle 8cm} 8cm, the width would be 3 c m {\displaystyle 3cm} 3cm.

Using the Diagonal and Length

Set up the formula for the diagonal of a rectangle. The formula is D = w 2 + l 2 {\displaystyle D={\sqrt {w^{2}+l^{2}}}} D={\sqrt {w^{{2}}+l^{{2}}}}, where D {\displaystyle D} D equals the length of the rectangle’s diagonal, l {\displaystyle l} l equals the length of the rectangle, and w {\displaystyle w} w equals the width of the rectangle. This method will only work if you are given the length of the diagonal and the length of the side of the rectangle. You might also see the formula written as D = w 2 + h 2 {\displaystyle D={\sqrt {w^{2}+h^{2}}}} D={\sqrt {w^{{2}}+h^{{2}}}}, where h {\displaystyle h} h equals the height of the rectangle and is used instead of length. The variables l {\displaystyle l} l and h {\displaystyle h} h refer to the same measurement.

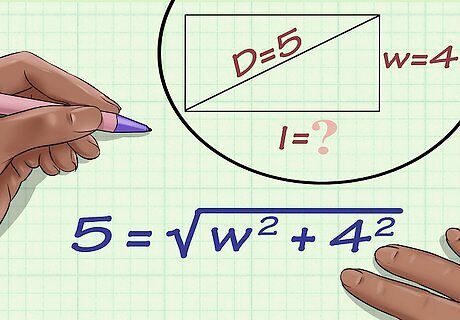
Plug the values for the diagonal and side length into the formula. Make sure you substitute for the correct variables. For example, if you are trying to find the width of a rectangle that has a diagonal length of 5 centimeters, and a side length of 4 centimeters, your formula will look like this: 5 = w 2 + 4 2 {\displaystyle 5={\sqrt {w^{2}+4^{2}}}} 5={\sqrt {w^{{2}}+4^{{2}}}}

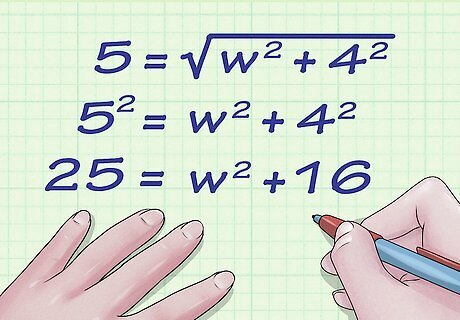
Square both sides of the formula. You need to do this to get rid of the square root sign, which makes isolating the width variable easier. For example: 5 = w 2 + 4 2 {\displaystyle 5={\sqrt {w^{2}+4^{2}}}} 5={\sqrt {w^{{2}}+4^{{2}}}} 5 2 = w 2 + 4 2 {\displaystyle 5^{2}=w^{2}+4^{2}} 5^{{2}}=w^{{2}}+4^{{2}} 25 = w 2 + 16 {\displaystyle 25=w^{2}+16} 25=w^{{2}}+16

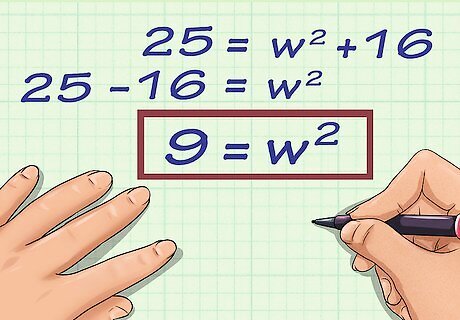
Isolate the w {\displaystyle w} w variable. To do this, you need to subtract the squared length from each side of the equation. For example, in the equation 25 = 16 + w 2 {\displaystyle 25=16+w^{2}} 25=16+w^{{2}}, you would subtract 16 from each side. 25 = 16 + w 2 {\displaystyle 25=16+w^{2}} 25=16+w^{{2}} 9 = w 2 {\displaystyle 9=w^{2}} 9=w^{{2}}

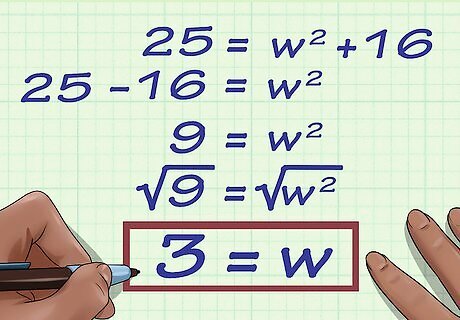
Solve for w {\displaystyle w} w. To do this, you need to find the square root of each side of the equation. For example: 9 = w 2 {\displaystyle {\sqrt {9}}={\sqrt {w^{2}}}} {\sqrt {9}}={\sqrt {w^{{2}}}} 3 = w {\displaystyle 3=w} 3=w

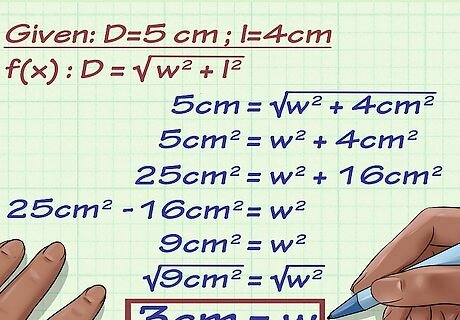
Write your final answer. Don’t forget to include the unit of measurement. For example, for a rectangle with a diagonal length of 5 c m {\displaystyle 5cm} 5cm and a side length of 4 c m {\displaystyle 4cm} 4cm, the width would be 3 c m {\displaystyle 3cm} 3cm.

Using Area or Perimeter and Relative Length

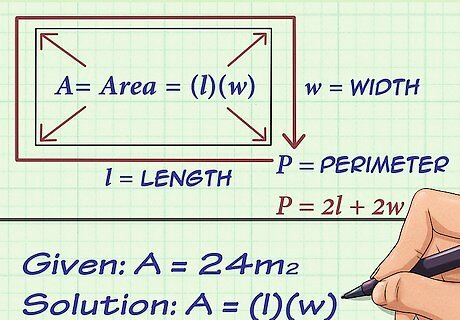
Set up the formula for area or perimeter of a rectangle. Which formula you use will depend on which measurement you are given. If you are given the area, set up the area formula. If you are given the perimeter, set up the perimeter formula. If you do not know the area or the perimeter, or the relationship between the length and the width, you cannot use this method. The formula for area is A = ( l ) ( w ) {\displaystyle A=(l)(w)} A=(l)(w). The formula for perimeter is P = 2 l + 2 w {\displaystyle P=2l+2w} P=2l+2w. For example, you might know that the area of a rectangle is 24 square centimeters, so you would set up the formula for area of a rectangle.

Write the expression that describes the relationship between the length and the width. Write your expression in terms of what l {\displaystyle l} l equals. The relationship might be given by stating how many times bigger one side is than the other, or how many units more or less it is. For example, you might know that the length is five centimeters longer than the width. Your expression for the length is then l = w + 5 {\displaystyle l=w+5} l=w+5.

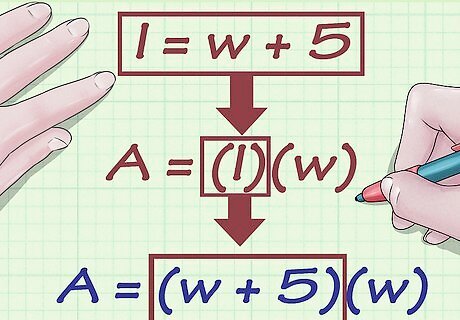
Replace the l {\displaystyle l} l variable in your area (or perimeter) formula with the expression for length. Your formula should now only contain the variable w {\displaystyle w} w, which means you can solve for the width. For example, if you know that area is 24 square centimeters, and that l = w + 5 {\displaystyle l=w+5} l=w+5, your formula will look like this: A = ( l ) ( w ) {\displaystyle A=(l)(w)} A=(l)(w) 24 = ( w + 5 ) ( w ) {\displaystyle 24=(w+5)(w)} 24=(w+5)(w)

Simplify the equation. Your simplified equation might take on various forms, depending on the relationship between the length and the width, and depending on whether you are working with area or perimeter. Think about setting up an equation that allows you to solve for w {\displaystyle w} w in the simplest way. For example, you can simplify 24 = ( w + 5 ) ( w ) {\displaystyle 24=(w+5)(w)} 24=(w+5)(w) to 0 = w 2 + 5 w − 24 {\displaystyle 0=w^{2}+5w-24} 0=w^{{2}}+5w-24.

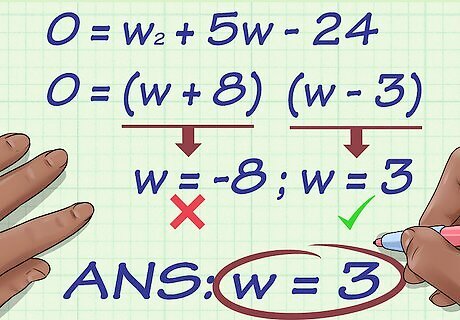
Solve for w {\displaystyle w} w. Again, how you solve for w {\displaystyle w} w will depend on your simplified equation. Use the basic rules of algebra and geometry to solve. You might need to use addition or division to solve, or you might need to factor a quadratic equation or use the quadratic formula to solve. For example, 0 = w 2 + 5 w − 24 {\displaystyle 0=w^{2}+5w-24} 0=w^{{2}}+5w-24 can be factored as follows: 0 = w 2 + 5 w − 24 {\displaystyle 0=w^{2}+5w-24} 0=w^{{2}}+5w-24 0 = ( w + 8 ) ( w − 3 ) {\displaystyle 0=(w+8)(w-3)} 0=(w+8)(w-3)You will then have two possible solutions for w {\displaystyle w} w: w = 3 {\displaystyle w=3} w=3 or w = − 8 {\displaystyle w=-8} w=-8. Since a rectangle cannot have a negative width, you can eliminate -8. So your solution is w = 3 {\displaystyle w=3} w=3.