views
Rules for Solving Diagonal Sudoku
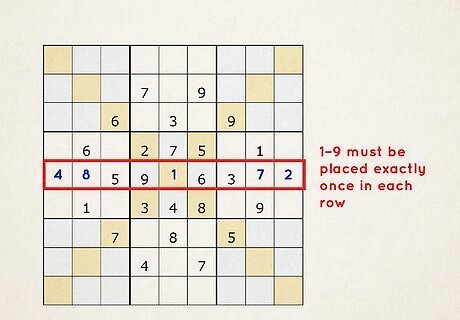
The numbers 1–9 must be placed exactly once in each row. A diagonal sudoku puzzle has 9 horizontal rows that each have 9 cells. You can’t repeat any of the numbers in a single row.

The numbers 1–9 must appear exactly once in each column. The 9 vertical columns have 9 cells each, so every number will only fit once.

The numbers 1–9 must be included exactly once in each 3 x 3 box. There are 9 boxes total in a sudoku puzzle that are marked by a thick outline.

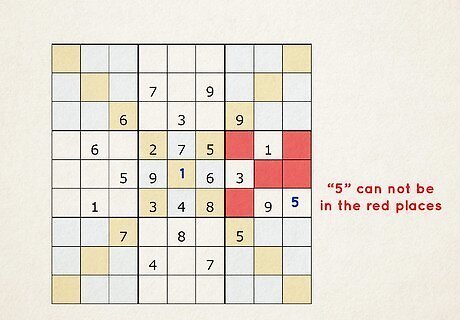
The numbers 1–9 must appear exactly once in the diagonals from each corner. The 2 main diagonals are 9 squares long. One runs from the top left to the bottom right corners, and the other goes from the top right to the bottom left corners. No other diagonal in the puzzle follows these constraints. Diagonal sudokus usually have lines drawn through the diagonals to remind you of this rule. Tougher diagonal sudoku puzzles have additional variants, such as only odd or even numbers appearing in the diagonals.
Use the given numbers to solve the puzzle without guessing. You’ll notice a handful of numbers already written in the puzzle to help you get started. Since there’s always a next logical step to take when you solve a sudoku puzzle, you won’t have to make any guesses to figure out the numbers.
Basic Strategies for Diagonal Sudoku
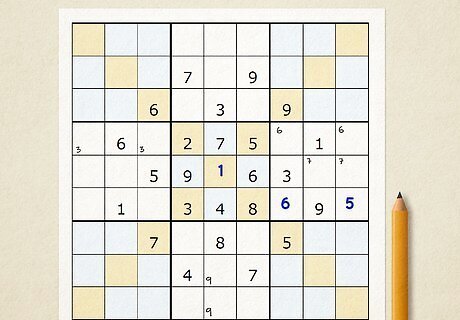
Write the possible numbers inside each cell in pencil. Start with any empty cell, and scan the row, column, and box that the cell is in to see which numbers are already there. If the cell is on one of the main diagonals, make sure you check for numbers there too. Write any remaining possible numbers inside the cell in pencil. Pencil in every other cell in the puzzle the same way. If the box already contains 2 and 4, the row has 3 and 7, the column has 5, and the diagonal has 9, then you know the cell must contain 1, 5, 6, or 9. As you keep doing sudoku puzzles, you'll start recognizing where numbers can go without writing all the numbers into the cells. Make sure you write the numbers small enough so you can fit all the possible options inside the cell.
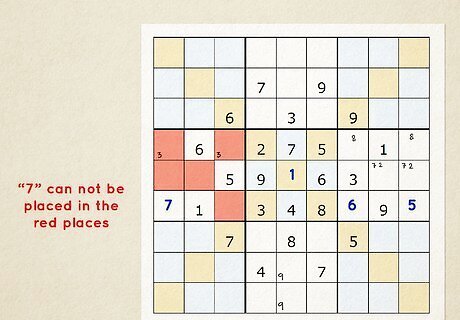
Fill in cells with only 1 possible number. Scan through your puzzle and look for cells where you only marked one number. Since no other numbers could fit in that cell, the number you wrote in has to be correct. Erase the small number you wrote in the cell and write the number in larger in ink so you know you're finished working on it. As you add a new number to the puzzle, check the row, column, and box for the same value. Since the number can’t be repeated in the same section, erase any other times you see the number.
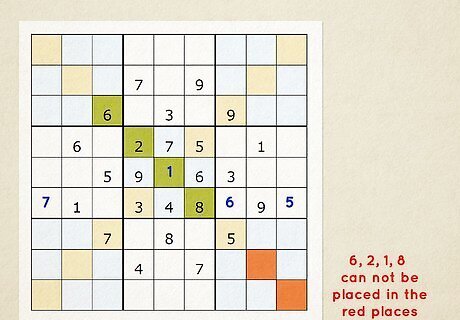
Look for numbers constrained to the diagonal. Focus on the 2 diagonals and look at the potential numbers that you’ve written in the empty cells. If you notice a pair of cells in the diagonal that are in a single 3 x 3 box are the only possible locations for a number, then it can’t be written in the diagonal in a different box. Similarly, if the only possible locations for a number in a diagonal are in a 3 x 3 box, you can eliminate that number from other cells in the same box.
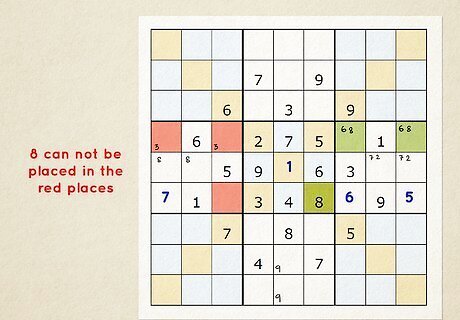
Check if any numbers are confined to a single row, column, or box. Scan one box at a time and look for cells that have the same number and share a single row or column. Using the process of elimination, you know that that number can’t be in the same row or column, so you can erase pencil marks with that value. These cells are called “locked candidates” because they’re locked into specific cells even if you don’t know exactly which one the number goes into.
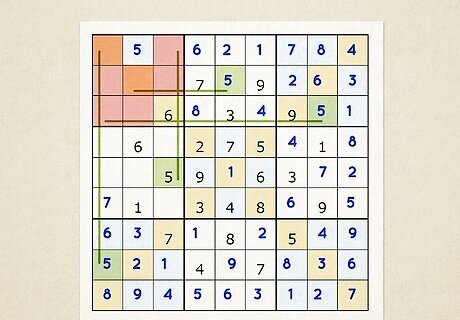
Scan for a pair of cells that both have the same numbers. If 2 cells in the same row, column, box, or diagonal have the same 2 numbers in them, then you can deduce that those are the only locations the numbers can go. Erase every other time the number appears in the same section. Cells with the same numbers in the same section are called “naked pairs.” You can also find “hidden pairs” if the numbers still only appear in 2 cells in the same section, even if the cell has other possible numbers. If 1 and 3 are only in a cell that has 1, 3, and 5 and another with 1, 3, and 6, then those numbers must be written there.
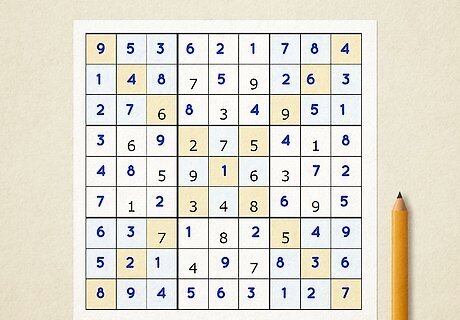
Eliminate potential numbers from rows and columns with the X-wing method. The X-Wing method only works if 2 cells in the same row could contain the same number, and if another row has the empty cells in the same position. If you draw an X connecting the top and bottom corners, the number can only appear in one set of the connected cells. The cells should form the corners of a rectangle if you drew lines between them. This method works because you know the number can’t be in the same column or row.















Comments
0 comment