How to Differentiate Polynomials

Differentiating Polynomial Terms

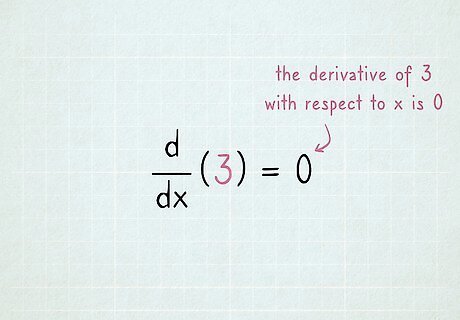
Differentiate any constant to zero. A constant is any ordinary number, with no variable involved—for example, 3, -16, or 2 / 3 {\displaystyle 2/3} {\displaystyle 2/3}. These are freebies in any differentiation problem, because their derivative is always 0. Just cross out that term and move on. Write this in the form d d x ( 3 ) = 0 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(3)=0} {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(3)=0}. This says "The derivative of 3 with respect to x is 0." The derivative of a term is the "rate of change" of that term: how quickly that term changes inside a function. Since a constant never changes (3 will always stay 3), its rate of change is always zero.

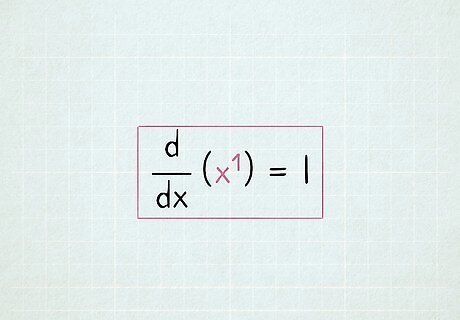
Differentiate x 1 {\displaystyle x^{1}} x^{1} to 1. The term x 1 {\displaystyle x^{1}} x^{1} (which we usually write as simply x {\displaystyle x} x) is another easy one to differentiate, once you know the rule. The derivative of x {\displaystyle x} x with respect to x {\displaystyle x} x is always 1. Write this as d d x ( x ) = 1 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(x)=1} {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(x)=1}. The notation dx means "derivative with respect to x." This means that we are changing the value of x, and seeing how much faster or slower the other term changes in response. In d d x ( x ) {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(x)} {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(x)}, we're comparing the change in x to the change in x. That's the same thing, which is why the rate of change is 1.

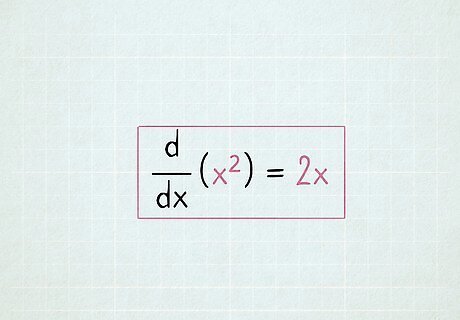
Write the derivative of x 2 {\displaystyle x^{2}} x^{2} as 2 x {\displaystyle 2x} 2x. The 2 in the exponent moves in front of the x to become the coefficient (the number multiplied by x).) Meanwhile, the x 2 {\displaystyle x^{2}} x^{{2}} gets reduced to x {\displaystyle x} x. Have you noticed a pattern? In the derivative, the value of the variable's exponent is always one lower than it was in the original term. x 2 {\displaystyle x^{2}} x^{2} gets "downgraded" to x 1 {\displaystyle x^{1}} x^{1} (which is x), and x 1 {\displaystyle x^{1}} x^{1} gets "downgraded" to x 0 {\displaystyle x^{0}} {\displaystyle x^{0}} (which equals 1). Since the value of the variable's exponent is called the "degree" of the polynomial, we can say that differentiating a term reduces the degree of that term by one.

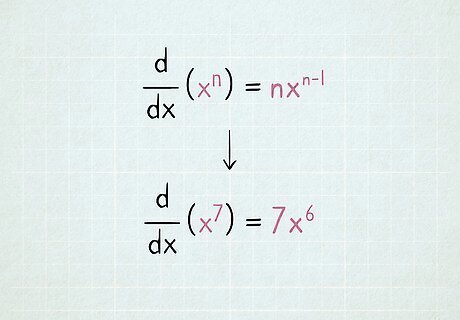
Differentiate x n {\displaystyle x^{n}} x^{n} to get n x n − 1 {\displaystyle nx^{n-1}} {\displaystyle nx^{n-1}}. Or in English: to differentiate a variable x raised to an exponent, write that exponent in front of x as a coefficient, then reduce the exponent by 1. This is one of the most useful differentiation rules. The rules for deriving x 2 {\displaystyle x^{2}} x^{2} and x {\displaystyle x} x above are actually just specific examples of this general rule. Example: what is d d x ( x 7 ) {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(x^{7})} {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(x^{7})} (the derivative of x 7 {\displaystyle x^{7}} {\displaystyle x^{7}} with respect to x)? The exponent, 7, becomes a coefficient in front of the term: 7 x ? {\displaystyle 7x^{?}} {\displaystyle 7x^{?}} The new exponent is one lower than the original, 7-1=6. The answer is 7 x 6 {\displaystyle 7x^{6}} {\displaystyle 7x^{6}}.

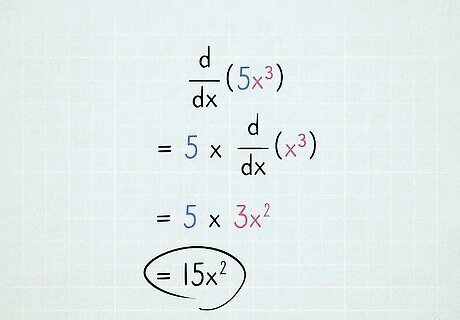
Multiply by the coefficient from the original term. The coefficient in front of the variable doesn't change when you differentiate the term. If you end up with more than one coefficient in your answer, multiply them together. Example: what is d d x ( 5 x 3 ) {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(5x^{3})} {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(5x^{3})}? d d x ( 5 x 3 ) = 5 × d d x ( x 3 ) {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(5x^{3})=5\times {\frac {\mathrm {d} }{\mathrm {d} x}}(x^{3})} {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(5x^{3})=5\times {\frac {\mathrm {d} }{\mathrm {d} x}}(x^{3})} (This means we can find the derivative of x 3 {\displaystyle x^{3}} x^{3}, then multiply our answer by 5.) To find the derivative of x 3 {\displaystyle x^{3}} x^{3}, make the exponent 3 a coefficient, then reduce the exponent by 1: d d x ( x 3 ) = 3 x 2 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(x^{3})=3x^{2}} {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(x^{3})=3x^{2}} Plug this back into your formula and multiply the two coefficients together: 5 × d d x ( x 3 ) = 5 × 3 x 2 = 15 x 2 {\displaystyle 5\times {\frac {\mathrm {d} }{\mathrm {d} x}}(x^{3})=5\times 3x^{2}=15x^{2}} {\displaystyle 5\times {\frac {\mathrm {d} }{\mathrm {d} x}}(x^{3})=5\times 3x^{2}=15x^{2}}

Differentiating Entire Polynomials

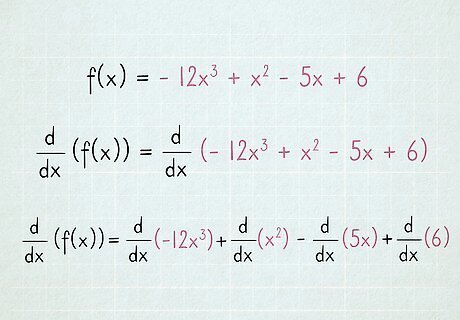
Treat each term as a separate problem. Polynomials contain multiple terms, added or subtracted together. To differentiate the polynomial, differentiate each term separately. You can leave all of the addition and subtraction symbols alone. For example, take f ( x ) = − 12 x 3 + x 2 − 5 x + 6 {\displaystyle f(x)=-12x^{3}+x^{2}-5x+6} {\displaystyle f(x)=-12x^{3}+x^{2}-5x+6}. The derivative, f ′ ( x ) {\displaystyle f'(x)} f'(x), is equal to the derivative of each term, added or subtracted as they were in the original. In mathematical terms, we can write this as: d d x ( f ( x ) ) = d d x ( − 12 x 3 + x 2 − 5 x + 6 ) {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(f(x))={\frac {\mathrm {d} }{\mathrm {d} x}}(-12x^{3}+x^{2}-5x+6)} {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(f(x))={\frac {\mathrm {d} }{\mathrm {d} x}}(-12x^{3}+x^{2}-5x+6)} = d d x ( − 12 x 3 ) + d d x ( x 2 ) − d d x ( 5 x ) + d d x ( 6 ) {\displaystyle ={\frac {\mathrm {d} }{\mathrm {d} x}}(-12x^{3})+{\frac {\mathrm {d} }{\mathrm {d} x}}(x^{2})-{\frac {\mathrm {d} }{\mathrm {d} x}}(5x)+{\frac {\mathrm {d} }{\mathrm {d} x}}(6)} {\displaystyle ={\frac {\mathrm {d} }{\mathrm {d} x}}(-12x^{3})+{\frac {\mathrm {d} }{\mathrm {d} x}}(x^{2})-{\frac {\mathrm {d} }{\mathrm {d} x}}(5x)+{\frac {\mathrm {d} }{\mathrm {d} x}}(6)}.

Get rid of the constant term. If there is a constant (a term without a variable), delete it. Differentiating always removes the constant term. In our example, 6 is the constant. d d x ( 6 ) = 0 {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(6)=0} {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}(6)=0}, so we can get rid of it. Careful: only terms with no variables are constants. This rule does not affect numbers that are multiplied by x or any other variable.

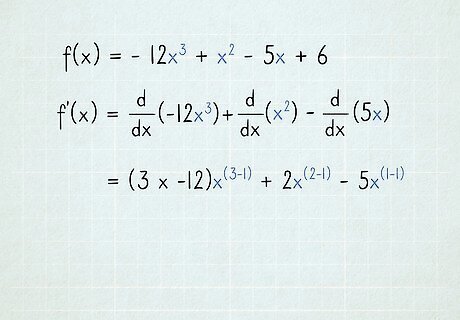
Move each variable's exponent to the front of the term. Remember, when we differentiate, each variable's exponent becomes a coefficient. If there is already a coefficient in front of the term, multiply the two coefficients together. f ′ ( x ) = d d x ( − 12 x 3 ) + d d x ( x 2 ) − d d x ( 5 x ) {\displaystyle f'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}(-12x^{3})+{\frac {\mathrm {d} }{\mathrm {d} x}}(x^{2})-{\frac {\mathrm {d} }{\mathrm {d} x}}(5x)} {\displaystyle f'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}(-12x^{3})+{\frac {\mathrm {d} }{\mathrm {d} x}}(x^{2})-{\frac {\mathrm {d} }{\mathrm {d} x}}(5x)} = ( 3 × − 12 ) x ? + 2 x ? − ( 1 × 5 ) x ? {\displaystyle =(3\times -12)x^{?}+2x^{?}-(1\times 5)x^{?}} {\displaystyle =(3\times -12)x^{?}+2x^{?}-(1\times 5)x^{?}} = − 36 x ? + 2 x ? − 5 x ? {\displaystyle =-36x^{?}+2x^{?}-5x^{?}} {\displaystyle =-36x^{?}+2x^{?}-5x^{?}} Since x = x 1 {\displaystyle x=x^{1}} {\displaystyle x=x^{1}}, we took the "1" exponent and moved it in front of the 5 x {\displaystyle 5x} 5x term. Since multiplying by 1 never changes the term, you can skip this step once you understand what's going on.

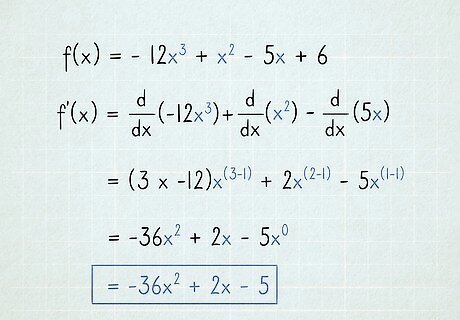
Lower each exponent by one degree. To do this, subtract 1 from each exponent in each variable term. f ′ ( x ) = − 36 x 3 − 1 + 2 x 2 − 1 − 5 x 1 − 1 {\displaystyle f'(x)=-36x^{3-1}+2x^{2-1}-5x^{1-1}} {\displaystyle f'(x)=-36x^{3-1}+2x^{2-1}-5x^{1-1}} = − 36 x 2 + 2 x 1 − 5 x 0 {\displaystyle =-36x^{2}+2x^{1}-5x^{0}} {\displaystyle =-36x^{2}+2x^{1}-5x^{0}} = − 36 x 2 + 2 x − 5 {\displaystyle =-36x^{2}+2x-5} {\displaystyle =-36x^{2}+2x-5} Remember that x 1 {\displaystyle x^{1}} x^{{1}} is the same as x {\displaystyle x} x. Also remember that anything raised to the zeroth power ( x 0 {\displaystyle x^{0}} x^{{0}}) equals 1.

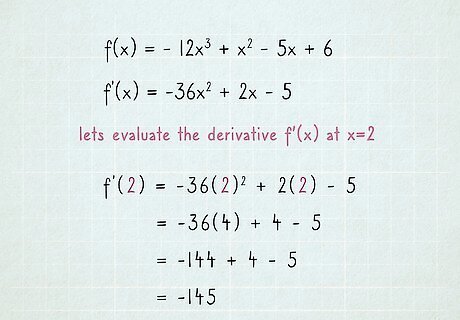
Find the value of the new equation at a given "x" value. You're already done with the differentiation, but there's a common next step in test problems. If you're asked to "evaluate the expression" for a value of x, all you need to do is replace each x in the new equation with the given value and solve. For example, evaluate the derivative f'(x) at x=2. The derivative equation we found is f ′ ( x ) = − 36 x 2 + 2 x − 5 {\displaystyle f'(x)=-36x^{2}+2x-5} {\displaystyle f'(x)=-36x^{2}+2x-5} f ′ ( 2 ) = − 36 ( 2 ) 2 + 2 ( 2 ) − 5 {\displaystyle f'(2)=-36(2)^{2}+2(2)-5} {\displaystyle f'(2)=-36(2)^{2}+2(2)-5} = − 36 ( 4 ) + 4 − 5 {\displaystyle =-36(4)+4-5} {\displaystyle =-36(4)+4-5} = − 144 + 4 − 5 {\displaystyle =-144+4-5} {\displaystyle =-144+4-5} = − 145 {\displaystyle =-145} {\displaystyle =-145} This answer relates back to the original function f(x). It tells us that, if we draw a tangent line to that function at x=2, the slope of that tangent line is -145.