How to Tell if Two Ratios Are in Proportion

Finding Equivalent Fractions

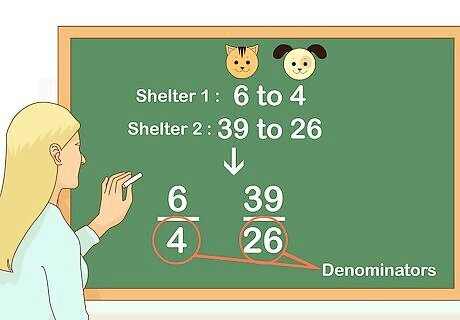
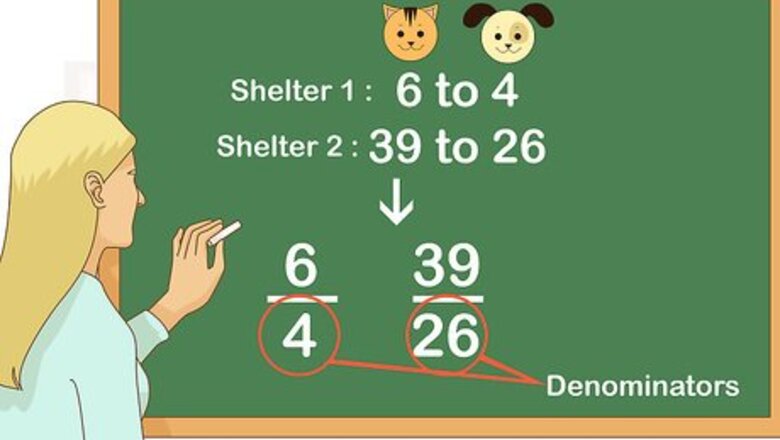
Identify the denominator of each ratio. Ratios can be expressed using a colon ( 1 : 2 {\displaystyle 1:2} 1:2), the word “to” ( 1 to 2 {\displaystyle {\text{1 to 2}}} {\text{1 to 2}}), or a fraction bar ( 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}}). Set up your ratios as fractions. The denominator is the number below the fraction bar. For example, if one shelter’s ratio of cats to dogs is 6 to 4, and another shelter’s ratio of cats to dogs is 39 to 26, you would rewrite the ratios as 6 4 {\displaystyle {\frac {6}{4}}} {\frac {6}{4}} and 39 26 {\displaystyle {\frac {39}{26}}} {\frac {39}{26}}. So, the denominators are 4 {\displaystyle 4} 4 and 26 {\displaystyle 26} 26.

Find the least common multiple for the two denominators. To find the least common multiple, look for the smallest multiple each denominator has in common. If there is no least common multiple, then the ratios cannot be in proportion and no further steps are required. For example, the denominators 4 and 26 are both multiples of 52.

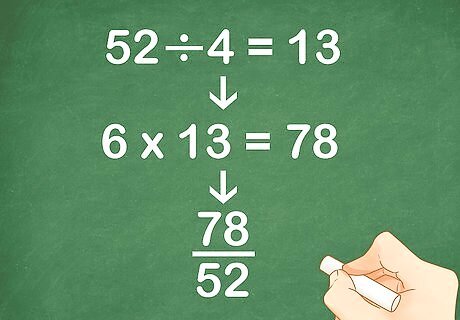
Write the equivalent fraction for the first ratio. To find the equivalent fraction, divide the least common multiple by the denominator. Multiply the numerator by this quotient. This will give you the new numerator of your equivalent fraction. For example, if the first ratio is 6 4 {\displaystyle {\frac {6}{4}}} {\frac {6}{4}}, you would divide the least common multiple (52) by 4: 52 ÷ 4 = 13 {\displaystyle 52\div 4=13} 52\div 4=13.So, you will multiply the numerator (6) by 13: 6 × 13 = 78 {\displaystyle 6\times 13=78} 6\times 13=78.So, your new fraction becomes 78 52 {\displaystyle {\frac {78}{52}}} {\frac {78}{52}}.

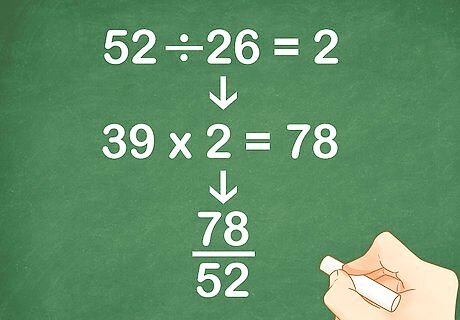
Write the equivalent fraction for the second ratio. Follow the same steps you did to find the equivalent fraction for the first ratio. For example, if the second ratio is 39 26 {\displaystyle {\frac {39}{26}}} {\frac {39}{26}}, you would divide the least common multiple (52) by 26: 52 ÷ 26 = 2 {\displaystyle 52\div 26=2} 52\div 26=2.So, you will multiply the numerator (39) by 2: 39 × 2 = 78 {\displaystyle 39\times 2=78} 39\times 2=78.So, your new fraction becomes 78 52 {\displaystyle {\frac {78}{52}}} {\frac {78}{52}}.

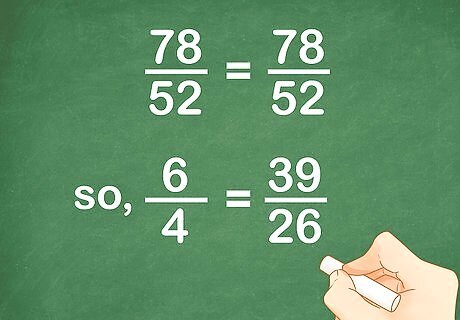
Compare the two equivalent fractions. If the two fractions are equal, then the two original ratios are in proportion. For example, 78 52 = 78 52 {\displaystyle {\frac {78}{52}}={\frac {78}{52}}} {\frac {78}{52}}={\frac {78}{52}}, so 6 4 = 39 26 {\displaystyle {\frac {6}{4}}={\frac {39}{26}}} {\frac {6}{4}}={\frac {39}{26}}

Using Cross Multiplication

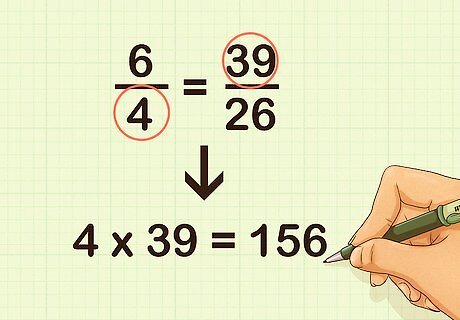
Set up the ratios as equivalent fractions. Ratios are sometimes expressed using a colon ( 1 : 2 {\displaystyle 1:2} 1:2) or the word “to” ( 1 to 2 {\displaystyle {\text{1 to 2}}} {\text{1 to 2}}). If your ratios are set up this way, turn them into fractions. For example, if you are comparing the ratios 6 to 4 and 39 to 26, set them up as follows: 6 4 = 39 26 {\displaystyle {\frac {6}{4}}={\frac {39}{26}}} {\frac {6}{4}}={\frac {39}{26}}.

Multiply the numerator of the first fraction and the denominator of the second fraction. Place this product to the right of the equation. For example, 6 × 26 = 156 {\displaystyle 6\times 26=156} 6\times 26=156: 6 4 = 39 26 156 {\displaystyle {\frac {\cancel {6}}{4}}={\frac {39}{\cancel {26}}}156} {\frac {{\cancel {6}}}{4}}={\frac {39}{{\cancel {26}}}}156

Multiply the denominator of the first fraction and the numerator of the second fraction. Place this product to the left of the equation. For example, 4 × 39 = 156 {\displaystyle 4\times 39=156} 4\times 39=156: 156 6 4 = 39 26 156 {\displaystyle 156{\frac {\cancel {6}}{\cancel {4}}}={\frac {\cancel {39}}{\cancel {26}}}156} 156{\frac {{\cancel {6}}}{{\cancel {4}}}}={\frac {{\cancel {39}}}{{\cancel {26}}}}156

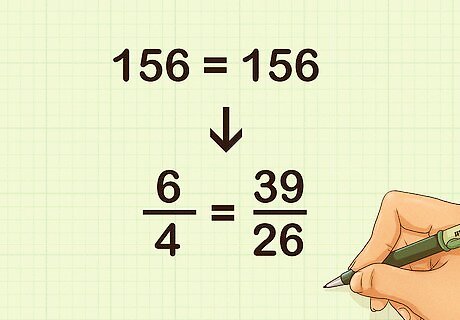
Compare the two products. If they are the same, then the ratios are in proportion. For example, since 156 = 156 {\displaystyle 156=156} 156=156, you know that 6 4 = 39 26 {\displaystyle {\frac {6}{4}}={\frac {39}{26}}} {\frac {6}{4}}={\frac {39}{26}}.

Finding a Missing Proportion

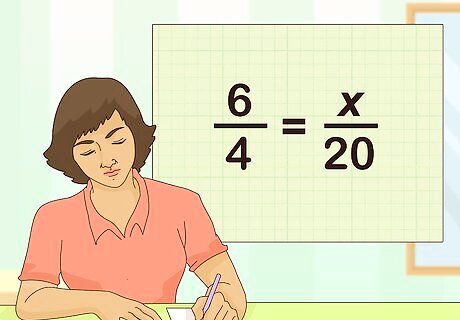
Set up the ratios as equivalent fractions. Ratios are sometimes expressed using a colon ( 1 : 2 {\displaystyle 1:2} 1:2) or the word “to” ( 1 to 2 {\displaystyle {\text{1 to 2}}} {\text{1 to 2}}). If your ratios are set up this way, turn them into fractions. Use a variable, such as x {\displaystyle x} x, to stand for the missing number For example, if you are baking cookies, and you need 6 cups of flour for every 4 batches of cookies, how many cups of flour do you need to make 20 batches of cookies? The first ratio is 6 4 {\displaystyle {\frac {6}{4}}} {\frac {6}{4}}. The second ratio is x 20 {\displaystyle {\frac {x}{20}}} {\frac {x}{20}}, since you are trying to find out how many cups of flour you need to make 20 batches of cookies. So your proportion will be set up like this: 6 4 = x 20 {\displaystyle {\frac {6}{4}}={\frac {x}{20}}} {\frac {6}{4}}={\frac {x}{20}}.

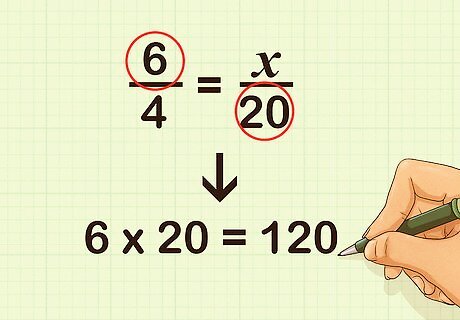
Multiply the numerator of the first fraction and the denominator of the second fraction. Place this product to the right of the equation. For example, 6 × 20 = 120 {\displaystyle 6\times 20=120} 6\times 20=120: 6 4 = x 20 120 {\displaystyle {\frac {\cancel {6}}{4}}={\frac {x}{\cancel {20}}}120} {\frac {{\cancel {6}}}{4}}={\frac {x}{{\cancel {20}}}}120

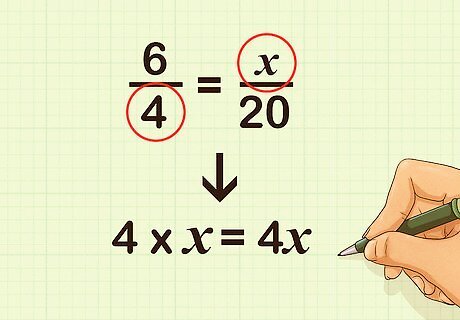
Multiply the denominator of the first fraction and the numerator of the second fraction. Place this product to the left of the equation. For example, 4 × x = 4 x {\displaystyle 4\times x=4x} 4\times x=4x: 4 x 6 4 = x 20 120 {\displaystyle 4x{\frac {\cancel {6}}{\cancel {4}}}={\frac {\cancel {x}}{\cancel {20}}}120} 4x{\frac {{\cancel {6}}}{{\cancel {4}}}}={\frac {{\cancel {x}}}{{\cancel {20}}}}120

Solve for x {\displaystyle x} x. This will give you the missing number in your second ratio. The two ratios are now in proportion. For example: 4 x = 120 {\displaystyle 4x=120} 4x=120 4 x 4 = 120 4 {\displaystyle {\frac {4x}{4}}={\frac {120}{4}}} {\frac {4x}{4}}={\frac {120}{4}} x = 30 {\displaystyle x=30} x=30.So, if you need 6 cups of flour for 4 batches of cookies, you will need 30 cups of flour for 20 batches of cookies. Thus, 6 4 {\displaystyle {\frac {6}{4}}} {\frac {6}{4}} and 30 20 {\displaystyle {\frac {30}{20}}} {\frac {30}{20}} are ratios in proportion.