views
Use a pencil.

This may seem obvious to you, but some folks don’t do this! It’s possible for adept players to solve easier sudokus with pen, but for harder puzzles it’s going to help a lot if you use pencil. Harder puzzles require a lot of testing and note-taking, and being able to erase your marks will make it easier to visually process what you’re doing. You can also write in the margins outside of the cells (the individual boxes of 9 squares inside of larger puzzle). Feel free to take notes or jot down reminders to yourself. Using pencil also allows you to draw on the puzzle. If you use any patterns or uniqueness tests, you may want to visually track what you’re doing by circling or drawing around given cells.
Note potential candidates in open squares.
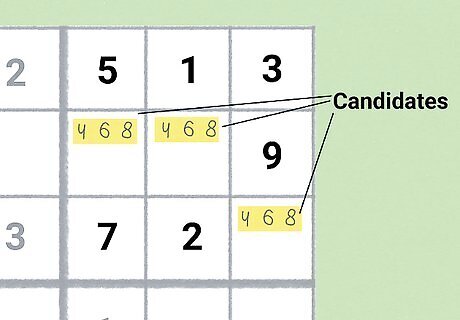
Taking notes is mandatory if you’re solving complex puzzles. Write potential candidates down lightly in open boxes. Most people use the corners, but you can use whatever method makes the most sense to you. This will help you narrow down choices, identify patterns, and avoid deadly patterns. If you’re a veteran, you probably already do this, but on the off-chance you don’t, it’s an essential way to play. Candidates refer to the potential solutions for a given square. If you know that square has to be a 6, 4, or 8, then 6, 4, and 8 are all candidates. It may feel like you’re making things harder by writing down every candidate, but the more information you have, the easier it will be to identify patterns and rule out incorrect answers. Some sudoku enthusiasts will “rank” their potential solutions by putting numbers they’re fairly confident in at the top corners, and numbers they’re less confident in at the bottom.
Scan the board to process the puzzle.
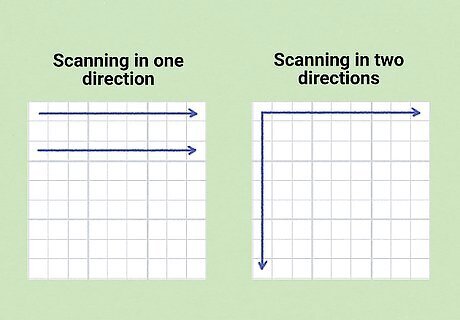
Take a minute to look over the board and take it all in. You’re probably not on a timer here, so don’t rush anything. Scan each cell to mentally map out and internalize the given numbers. This will get you comfortable with this specific puzzle, and keep you from making an early move that accidentally throws off the entire course of the puzzle. There are two popular scanning techniques: one direction and two directions. Scanning in one direction involves viewing the cells from left-to-right and up-to down. Scanning in two directions involves looking at perpendicular rows and columns together to process early combinations. If anything stands out to you as exceptionally obvious once you’re done scanning the given numbers, go ahead and fill in the squares you’re 100% confident in.
Start with the obvious singles.
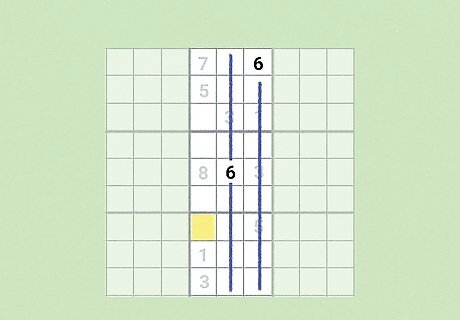
Naked and hidden singles are the easiest squares to solve. A naked single is when a number can only go in one possible cell. A hidden single is when there is only cell for a given candidate. These singles are easy to identify, so spend a few minutes scanning each row, column, and cell for any squares with only one possible solution. Cells refer to the collection of 9 squares that are inside of each sudoku puzzle. For example, if there’s a 6 in the middle square of the center cell and a 6 in the righthand column of the top-center cell, but there is only one available square in the left-hand column of the bottom-center cell, then a 6 has to go there!
Revisit your candidates after you solve singles.
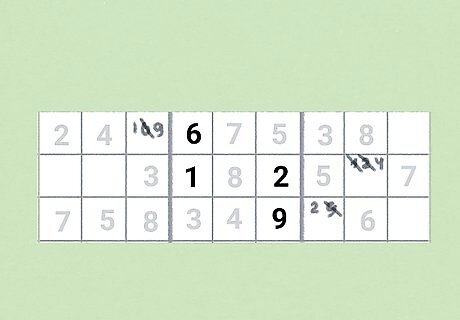
After you fill a square in, use the rule of one to find additional singles. Whenever you solve a square, double-check the other candidates in the number’s row, column, and cell. Erase any notes you made that would violate the rule of one (there can only be one instance of a number in every row, column, and cell). This may give you even more hidden and naked singles. Keep doing this over and over again until you’ve exhausted all of the potential singles on the board.
Identify naked or hidden pairs.
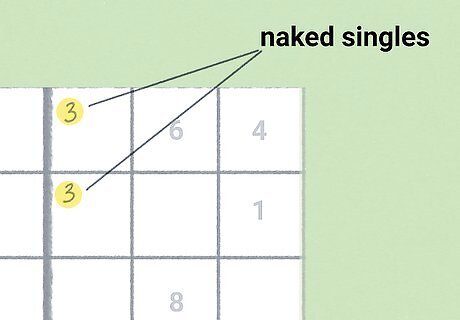
After hidden and naked singles, pairs are the most helpful. If you have two squares inside of a cell that could only be one of two numbers, you have a naked pair. This may seem unsolvable right now (since there’s no way to know which square takes which candidate), but they’re helpful for the cell you’re in. Use the pair to deduce which potential candidates exist for the other squares in that cell. By eliminating the pair, you may end up with a hidden single! For example, let’s say you’ve got two 3s written down in the top two rows of squares in the top right cell. This is a naked pair. On the top left cell, a 3 may be able to go in any square right now. Since your pair rules out the bottom row in the top left, you can cross those candidates out. If this reveals a single, you’ve got a new square to fill in!
Move on to triples and quads.
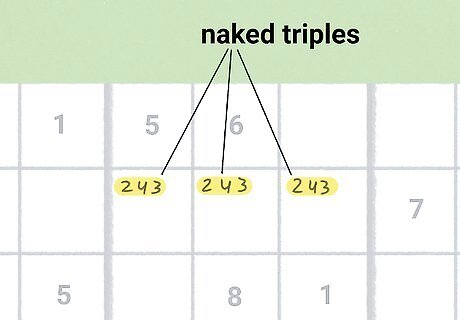
Exhausting pairs and singles should reveal naked triples and quads. Whenever you reveal 3 potential candidates across 2 or more squares in a given row, column, or cell, you’ve got a triple. You can use triples to reveal hidden singles the same way you used naked and hidden pairs. Once you’ve exhausted all of your pairs, take a look at the triples and quads you spot. At this point, with a large number of candidates crossed off of potential squares, you may be able to fill in additional squares. Quads are much rarer, and they’re less helpful in a way since they don’t let you narrow down a large number of candidates all at once, but if you spot one, it’s worth investigating. Solving single squares can also turn quads into triples or pairs, so don’t forget about these!
Identify patterns in the remaining numbers.
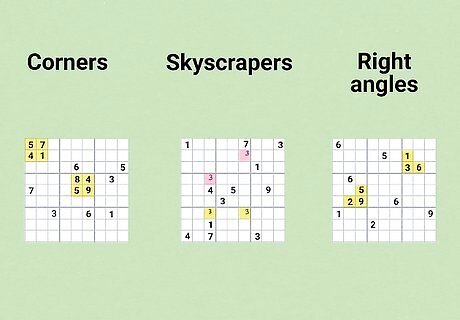
There are a handful of patterns most players look for at this point. Patterns refer to configurations of solved squares that help players regularly solve a sequence of candidates. There are a bunch of different patterns out there, but if you can spot one, they’ll typically help you solve some element of the puzzle that you’re struggling with. A few common patterns include: Corners (a collection of 4 solved squares in any of the 4 corners). Corner patterns help eliminate a ton of potential candidates in the rows and columns connected to it. Revisit these regularly to make sure you don’t provide a false solution. Skyscrapers (two rows or columns of a given candidate that are unequal in length). This pattern can help you isolate rows and columns to solve entire rows or columns of the puzzle. Right angles (any 3 given numbers in an L-shape inside of a cell). Right angles give you a lot of information regarding the empty columns and rows in the cell they’re in, which can help you cancel out incorrect candidates in the adjacent cells.
Scan for x-wings to eliminate false candidates.
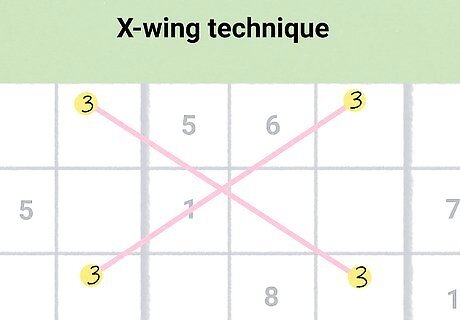
The x-wing technique can be used to remove a ton of potential answers. If you identify a set of 4 identical candidates that form a rectangle across multiple cells, you can use the x-wing technique. Since 2 identical numbers cannot be placed in the same row or column, you know that one “wing” has to be correct, and the other cannot be. Once you identify the x-wing, scan the cells, columns, and rows of the two wings and eliminate any candidates that would invalidate one of your wings. Remember, this only works if the candidates are located in different cells. You cannot use an x-wing if one of the wing pairs are in the same cell. This is easiest to visualize when the candidates are really close together, but the rectangular pattern required to use this technique could theoretically involve the 4 outermost corners of the puzzle.
Identify swordfish patterns to solve tough parallels.
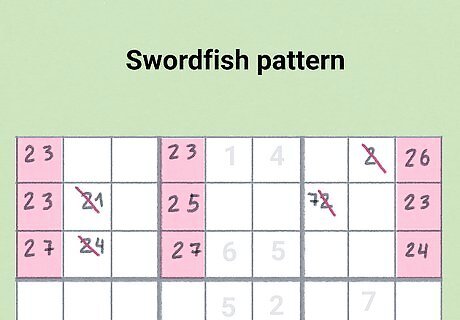
This is a variation of the x-wing that can get you out of tough locks. A swordfish occurs when 3 rows or columns contain 2 (or 3) cells that hold matching and locked candidates. If the candidates repeat, they cannot overlap and there must be one combination where the rule of one is not violated. Finding swordfishes can be kind of challenging since it requires a closed chain of 6 candidates with a redundant candidate in each row and column.
Use uniqueness tests to avoid deadly patterns.
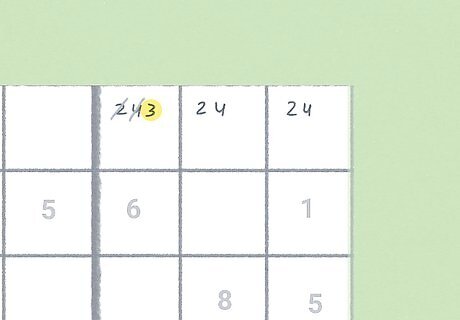
These tests help you avoid impossible candidate compositions. Deadly patterns refer to potential points in a puzzle where more than one solution can be equally viable based on the remaining candidates. These patterns stop a puzzle in their tracks, but uniqueness tests can help you avoid these gaps. At junctures where you risk a potential deadly pattern, use uniqueness tests to rule out false solutions. Variations include: If only one square in a given cell contains multiple candidates, you can eliminate the other candidates from that cell. This is the simplest version of a uniqueness test. If you have two triples in a cell, but one of the candidates appears a third time in a different square in that cell, you can eliminate it from the triples to reveal a naked pair. If you have two cells in a rectangle with one extra candidate, you can eliminate that candidate from any rows or columns in the adjacent cells.
Skip a square or cell if you get stuck.
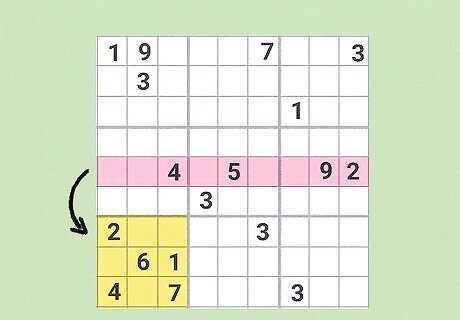
If you’re caught up on a square or cell, take a break from that area. If a sudoku is valid and solvable, it will (usually) require zero guesswork. There should always be an area somewhere on the board where you can methodically deduce an answer. If you find yourself totally stuck on a row, column, or set of candidates, take a break and look elsewhere. You may solve some other area of the puzzle and find the answer you were digging for suddenly revealed. It can also just help to return to an area with a fresh eye. If you get stuck, you’re going to get frustrated. Taking a break and moving on will allow you to return with a new attitude that may help you find a solution.
Double-check solved sections with the 45 rule.
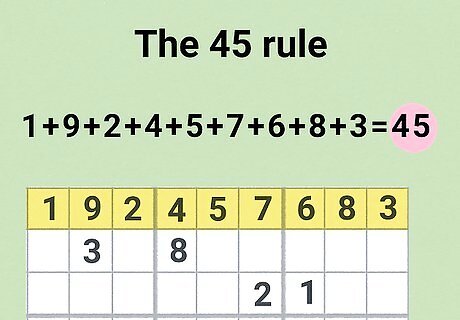
If you solve a row, column, or cell, use the 45 rule to confirm the solution. If you solve a part of the puzzle but you simply can’t find an answer to another part of the puzzle and it seems impossible, check your work. Any solved row, column, or cell should add up to 45. If you made a mistake and doubled-up your answers somewhere, it will keep you from solving other portions of the puzzle, so check your work! If you did make a mistake somewhere, it can create a snowball effect where you suddenly have incorrect answers everywhere. If it’s a super difficult sudoku, calculate each row, column, or cell as soon as you solve it to make sure you haven’t made an obvious mistake.



















Comments
0 comment