How to Find the Diagonal of a Square Using Its Area

Finding the Length of One Side

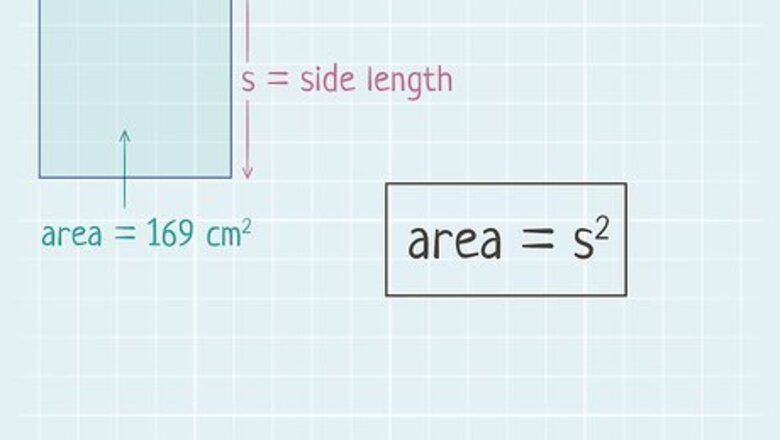
Set up the formula for the area of a square. The formula is Area = s 2 {\displaystyle {\text{Area}}=s^{2}} {\text{Area}}=s^{{2}}, where s {\displaystyle s} s equals the length of one side of the square. In order to find the length of the diagonal, you first need to find the side length of the square. The area of a rectangle is found by multiplying its length and width, but since a square rectangle has four equal side lengths, you can use this shortened formula for its area.

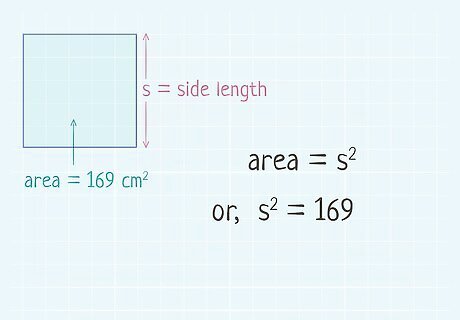
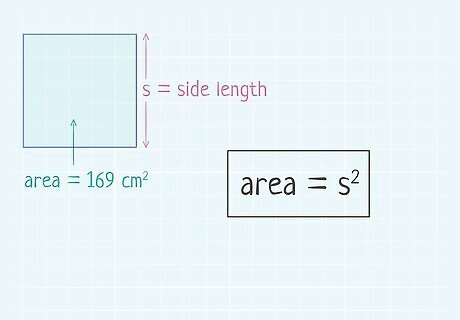
Plug the area into the formula. Make sure you put the value on the left side of the equation. Do not substitute for s {\displaystyle s} s. If you don’t know the area of the square, you cannot use this method. For example, you might need to find the diagonal length of a square that has an area of 169 square centimeters. So, your equation will look like this: 169 = s 2 {\displaystyle 169=s^{2}} 169=s^{{2}}.

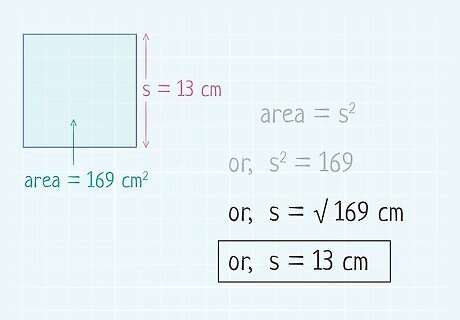
Find the square root of both sides of the equation. Taking the square root of both sides will give you the side length of the square. The easiest way to calculate a square root of a number is to use the x {\displaystyle {\sqrt {x}}} {\sqrt {x}} function on a calculator. You can also calculate a square root by hand. Remember that when finding the square root of a squared variable, the answer is simply the variable. For example: 169 = s 2 {\displaystyle 169=s^{2}} 169=s^{{2}} 169 = s 2 {\displaystyle {\sqrt {169}}={\sqrt {s^{2}}}} {\sqrt {169}}={\sqrt {s^{{2}}}} 13 = s {\displaystyle 13=s} 13=sSo, a square with an area of 169 square centimeters has a side length of 13 cm.

Calculating the Length of the Diagonal

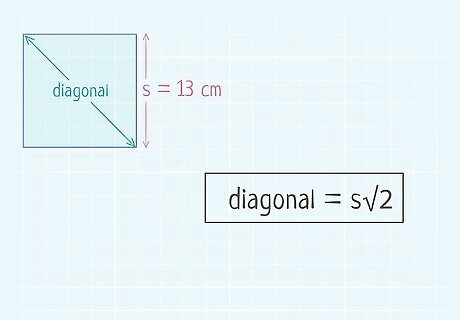
Set up the formula for the diagonal of a square. The formula is Diagonal = s 2 {\displaystyle {\text{Diagonal}}=s{\sqrt {2}}} {\text{Diagonal}}=s{\sqrt {2}}, where s {\displaystyle s} s is the length of one of the square’s sides. This formula is derived from the Pythagorean Theorem. The diagonal divides a square into two right triangles. So, using the side lengths and the Pythagorean Theorem, you get the formula s 2 + s 2 = c 2 {\displaystyle s^{2}+s^{2}=c^{2}} s^{{2}}+s^{{2}}=c^{{2}}, which simplifies to s 2 = c {\displaystyle s{\sqrt {2}}=c} s{\sqrt {2}}=c.

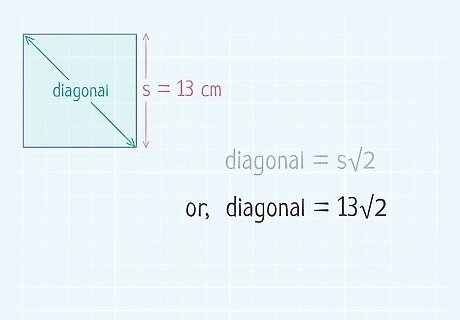
Plug the side length into the formula. Substitute for the variable s {\displaystyle s} s. You should have calculated the side length previously. For example, if you found that the side length of a square is 13 centimeter (5.1 in), your equation will look like this: Diagonal = 13 2 {\displaystyle {\text{Diagonal}}=13{\sqrt {2}}} {\text{Diagonal}}=13{\sqrt {2}}

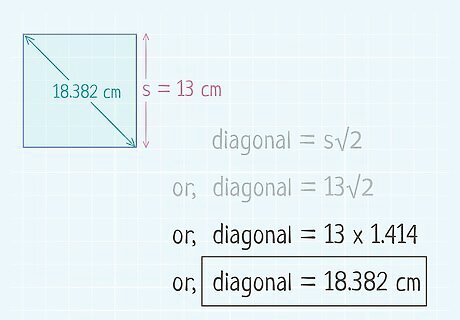
Multiply the side length by the square root of 2. The square root of 2 is about 1.414. You can also use a calculator to find a more precise answer. Calculating the side length by 2 {\displaystyle {\sqrt {2}}} {\sqrt {2}} gives you the length of the square’s diagonal. For example: Diagonal = 13 2 {\displaystyle {\text{Diagonal}}=13{\sqrt {2}}} {\text{Diagonal}}=13{\sqrt {2}} Diagonal = 13 ( 1.414 ) {\displaystyle {\text{Diagonal}}=13(1.414)} {\text{Diagonal}}=13(1.414) Diagonal = 18.382 {\displaystyle {\text{Diagonal}}=18.382} {\text{Diagonal}}=18.382So, the length of the square's diagonal is about 18.38 cm.

Completing Sample Problems

Try this problem. A square has an area of 120 square centimeters. What is the length of its diagonal? Find the side length of the square by using the formula Area = s 2 {\displaystyle {\text{Area}}=s^{2}} {\text{Area}}=s^{{2}}: 120 = s 2 {\displaystyle 120=s^{2}} 120=s^{{2}} 120 = s 2 {\displaystyle {\sqrt {120}}={\sqrt {s^{2}}}} {\sqrt {120}}={\sqrt {s^{{2}}}} 10.95 = s {\displaystyle 10.95=s} 10.95=s Plug the side length into the formula Diagonal = s 2 {\displaystyle {\text{Diagonal}}=s{\sqrt {2}}} {\text{Diagonal}}=s{\sqrt {2}}: Diagonal = 10.95 2 {\displaystyle {\text{Diagonal}}=10.95{\sqrt {2}}} {\text{Diagonal}}=10.95{\sqrt {2}} Diagonal = 10.95 ( 1.414 ) {\displaystyle {\text{Diagonal}}=10.95(1.414)} {\text{Diagonal}}=10.95(1.414) Diagonal = 15.4833 {\displaystyle {\text{Diagonal}}=15.4833} {\text{Diagonal}}=15.4833So, the length of the diagonal is about 15.5 cm.

Find the distance between opposite corners. The corners are at the northwest and southeast corners of a square field. The field has an area of 16,000 square feet. The distance between opposite corners of a square is the length of the diagonal. So first find the side length using the area formula: Area = s 2 {\displaystyle {\text{Area}}=s^{2}} {\text{Area}}=s^{{2}} 16 , 000 = s 2 {\displaystyle 16,000=s^{2}} 16,000=s^{{2}} 16 , 000 = s 2 {\displaystyle {\sqrt {16,000}}={\sqrt {s^{2}}}} {\sqrt {16,000}}={\sqrt {s^{{2}}}} 126.49 = s {\displaystyle 126.49=s} 126.49=s Plug the side length into the formula Diagonal = s 2 {\displaystyle {\text{Diagonal}}=s{\sqrt {2}}} {\text{Diagonal}}=s{\sqrt {2}}: Diagonal = 126.49 2 {\displaystyle {\text{Diagonal}}=126.49{\sqrt {2}}} {\text{Diagonal}}=126.49{\sqrt {2}} Diagonal = 126.49 ( 1.414 ) {\displaystyle {\text{Diagonal}}=126.49(1.414)} {\text{Diagonal}}=126.49(1.414) Diagonal = 178.86 {\displaystyle {\text{Diagonal}}=178.86} {\text{Diagonal}}=178.86So, the length of the diagonal is about 179 feet.

Compare two diagonals. The diagonal of rhombus is 12 feet (3.7 m). How does its length compare to the diagonal of a square with an area of 72.25 square feet? Find the square’s side length by using the area formula: Area = s 2 {\displaystyle {\text{Area}}=s^{2}} {\text{Area}}=s^{{2}} 72.25 = s 2 {\displaystyle 72.25=s^{2}} 72.25=s^{{2}} 72.25 = s 2 {\displaystyle {\sqrt {72.25}}={\sqrt {s^{2}}}} {\sqrt {72.25}}={\sqrt {s^{{2}}}} 8.5 = s {\displaystyle 8.5=s} 8.5=s Plug the side length into the formula Diagonal = s 2 {\displaystyle {\text{Diagonal}}=s{\sqrt {2}}} {\text{Diagonal}}=s{\sqrt {2}}: Diagonal = 8.5 2 {\displaystyle {\text{Diagonal}}=8.5{\sqrt {2}}} {\text{Diagonal}}=8.5{\sqrt {2}} Diagonal = 8.5 ( 1.414 ) {\displaystyle {\text{Diagonal}}=8.5(1.414)} {\text{Diagonal}}=8.5(1.414) Diagonal = 12.02 {\displaystyle {\text{Diagonal}}=12.02} {\text{Diagonal}}=12.02So, the length of the square’s diagonal is about 12 feet (4 m). This means that the diagonal of the rhombus is about the same length.