
views
speed
=
distance
time
{\displaystyle {\text{speed}}={\frac {\text{distance}}{\text{time}}}}
. But sometimes you are given two different speeds used for some periods of time, or over some distances. In these instances, other formulas exist for calculating the average speed. These types of problems might be useful to you in real life, and often appear on standardized tests, so it is helpful to learn these formulas and methods.
Given One Distance and One Time Period
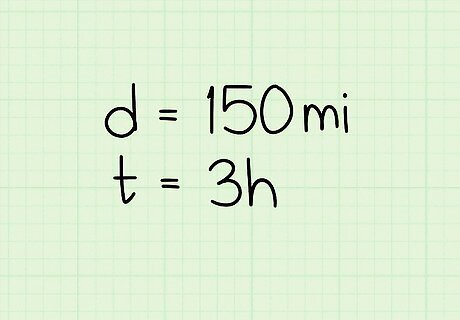
Assess what information you are given. Use this method if you know: the total distance covered by one person or vehicle; and the total time it took that person or vehicle to cover the distance. For example: If Ben traveled 150 miles in 3 hours, what was his average speed?
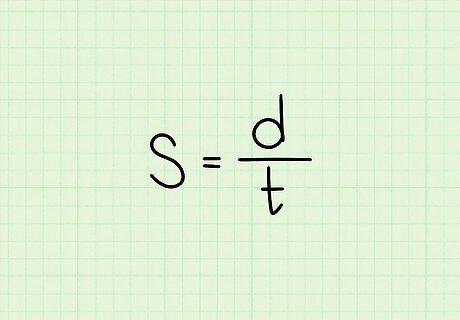
Set up the formula for speed. The formula is S = d t {\displaystyle S={\frac {d}{t}}} S={\frac {d}{t}}, where S {\displaystyle S} S equals the average speed, d {\displaystyle d} d equals the total distance, and t {\displaystyle t} t equals the total time.
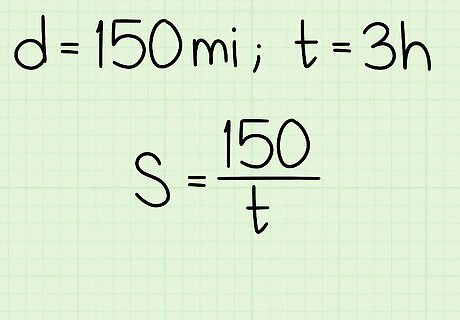
Plug the distance into the formula. Remember to substitute for the variable d {\displaystyle d} d. For example, if Ben drives 150 total miles, your formula will look like this: S = 150 t {\displaystyle S={\frac {150}{t}}} S={\frac {150}{t}}.
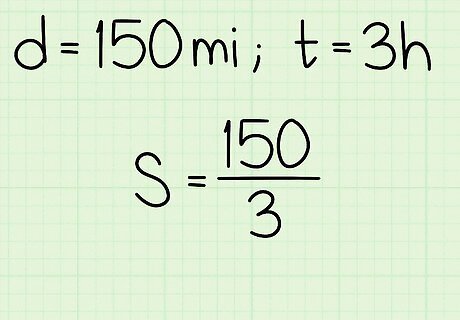
Plug the time into the formula. Remember to substitute for the variable t {\displaystyle t} t. For example, if Ben drives for 3 hours, your formula will look like this: S = 150 3 {\displaystyle S={\frac {150}{3}}} S={\frac {150}{3}}.

Divide the distance by the time. This will give you the average speed per unit of time, usually hour. For example: S = 150 3 {\displaystyle S={\frac {150}{3}}} S={\frac {150}{3}} S = 50 {\displaystyle S=50} S=50So, if Ben traveled 150 miles in 3 hours, his average speed is 50 miles per hour.
Given Multiple Distances in Different Amounts of Time
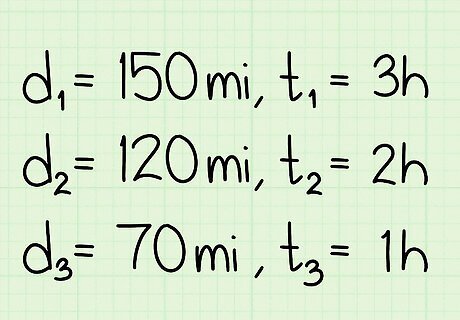
Assess what information you are given. Use this method if you know: multiple distances that were traveled; and the amount of time it took to travel each of those distances. For example: If Ben traveled 150 miles in 3 hours, 120 miles in 2 hours, and 70 miles in 1 hour, what was his average speed for the entire trip?
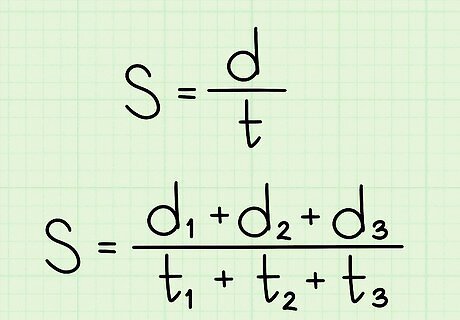
Set up the formula for average speed. The formula is S = d t {\displaystyle S={\frac {d}{t}}} S={\frac {d}{t}}, where S {\displaystyle S} S equals the average speed, d {\displaystyle d} d equals the total distance, and t {\displaystyle t} t equals the total time.

Determine the total distance. To do this, add up the number of miles traveled during the entire trip. Substitute this value for d {\displaystyle d} d in the formula. For example, If Ben traveled 150 miles, 120 miles, and 70 miles, you would determine the total speed by adding the three distances together: 150 + 120 + 70 = 340 {\displaystyle 150+120+70=340} 150+120+70=340. So, your formula will look like this: S = 340 t {\displaystyle S={\frac {340}{t}}} S={\frac {340}{t}}.
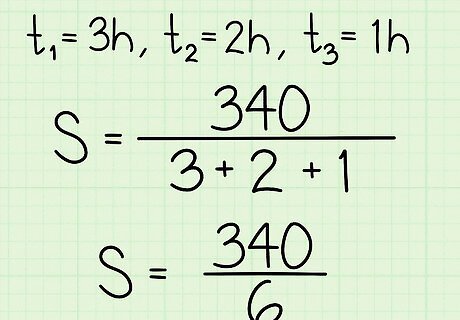
Determine the total time. To do this, add up the times, usually hours, that were spent traveling. Substitute this value for t {\displaystyle t} t in the formula. For example, If Ben for 3 hours, 2 hours, and 1 hour, you would determine the total time by adding the three times together: 3 + 2 + 1 = 6 {\displaystyle 3+2+1=6} 3+2+1=6. So, your formula will look like this: S = 340 6 {\displaystyle S={\frac {340}{6}}} S={\frac {340}{6}}.

Divide the total distance traveled by the total time spent traveling. This will give you your average speed. For example: S = 340 6 {\displaystyle S={\frac {340}{6}}} S={\frac {340}{6}} S = 56.67 {\displaystyle S=56.67} S=56.67. So if Ben traveled 150 miles in 3 hours, 120 miles in 2 hours, and 70 miles in 1 hour, his average speed was about 57 mph.
Given Multiple Speeds for Different Amounts of Time

Assess what information you are given. Use this method if you know: multiple speeds used to travel; and the amount of time each of those speeds was traveled for. For example: For example: If Ben traveled 50 mph for 3 hours, 60 mph for 2 hours, and 70 mph for 1 hour, what was his average speed for the entire trip?
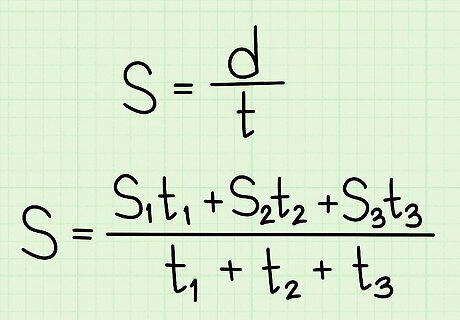
Set up the formula for average speed. The formula is S = d t {\displaystyle S={\frac {d}{t}}} S={\frac {d}{t}}, where S {\displaystyle S} S equals the average speed, d {\displaystyle d} d equals the total distance, and t {\displaystyle t} t equals the total time.
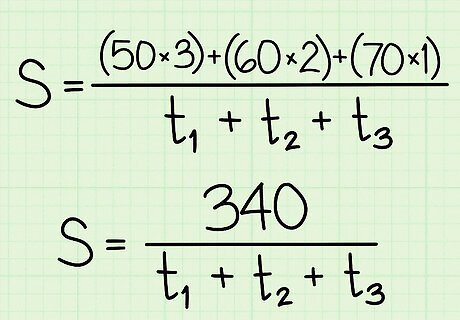
Determine the total distance. To do this, separately multiply each speed by each time period. This will give you the distance traveled for each section of the trip. Add up these distances. Substitute this sum for d {\displaystyle d} d in the formula. For example:50 mph for 3 hours = 50 × 3 = 150 miles {\displaystyle 50\times 3=150{\text{miles}}} 50\times 3=150{\text{miles}}60 mph for 2 hours = 60 × 2 = 120 miles {\displaystyle 60\times 2=120{\text{miles}}} 60\times 2=120{\text{miles}}70 mph for 1 hour = 70 × 1 = 70 miles {\displaystyle 70\times 1=70{\text{miles}}} 70\times 1=70{\text{miles}}So, the total distance is 150 + 120 + 70 = 340 miles . {\displaystyle 150+120+70=340{\text{miles}}.} 150+120+70=340{\text{miles}}. So, your formula will look like this: S = 340 t {\displaystyle S={\frac {340}{t}}} S={\frac {340}{t}}
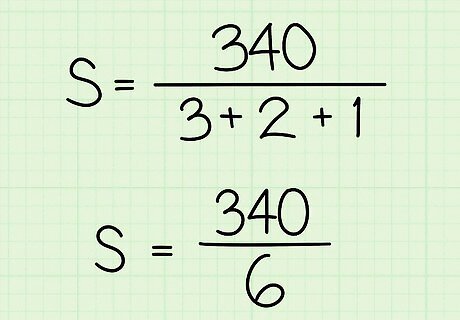
Determine the total time. To do this, add up the times, usually hours, that were spent traveling. Substitute this value for t {\displaystyle t} t in the formula. For example, If Ben for 3 hours, 2 hours, and 1 hour, you would determine the total time by adding the three times together: 3 + 2 + 1 = 6 {\displaystyle 3+2+1=6} 3+2+1=6. So, your formula will look like this: S = 340 6 {\displaystyle S={\frac {340}{6}}} S={\frac {340}{6}}.

Divide the total distance traveled by the total time spent traveling. This will give you your average speed. For example: S = 340 6 {\displaystyle S={\frac {340}{6}}} S={\frac {340}{6}} S = 56.67 {\displaystyle S=56.67} S=56.67. So if Ben traveled 50 mph for 3 hours, 60 mph for 2 hours, and 70 mph for 1 hour, his average speed was about 57 mph.
Given Two Speeds for Half the Time
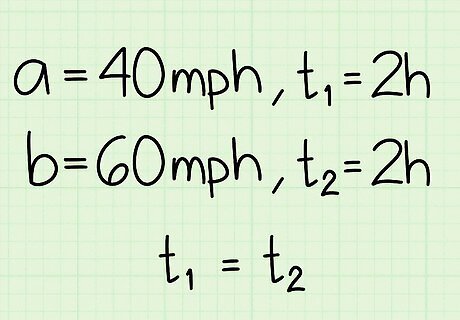
Assess what information you are given. Use this method if you know: two or more different speeds; and that those speeds were traveled for the same amount of time. For example, if Ben drives 40 mph for 2 hours, and 60 mph for another 2 hours, what is his average speed for the entire trip?
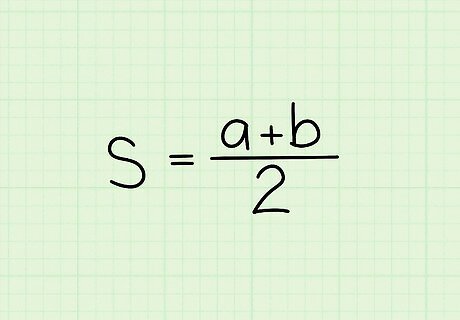
Set up the formula for average speed given two speeds used for the same amount of time. The formula is s = a + b 2 {\displaystyle s={\frac {a+b}{2}}} s={\frac {a+b}{2}}, where s {\displaystyle s} s equals the average speed, a {\displaystyle a} a equals the speed for the first half of the time, and b {\displaystyle b} b equals the speed for the second half of the time. In these types of problems, It doesn’t matter for how long each speed is driven, as long as each speed is used for half the total duration of time. You can modify the formula if you are given three or more speeds for the same amount of time. For example, s = a + b + c 3 {\displaystyle s={\frac {a+b+c}{3}}} s={\frac {a+b+c}{3}} or s = a + b + c + d 4 {\displaystyle s={\frac {a+b+c+d}{4}}} s={\frac {a+b+c+d}{4}}. As long as the speeds were used for the same amount of time, your formula can follow this pattern.
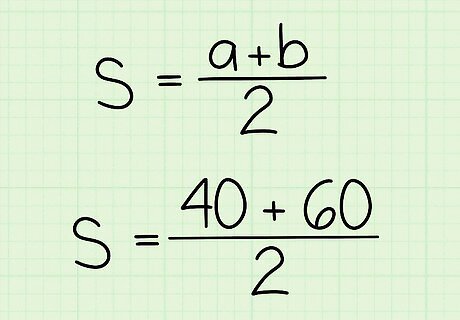
Plug the speeds into the formula. It doesn’t matter which speed you substitute for a {\displaystyle a} a and which you substitute for b {\displaystyle b} b. For example, if the first speed is 40 mph, and the second speed is 60 mph, your formula will look like this: s = 40 + 60 2 {\displaystyle s={\frac {40+60}{2}}} s={\frac {40+60}{2}}.

Add the two speeds together. Then, divide the sum by two. This will give you the average speed for the entire trip. For example: s = 40 + 60 2 {\displaystyle s={\frac {40+60}{2}}} s={\frac {40+60}{2}} s = 100 2 {\displaystyle s={\frac {100}{2}}} s={\frac {100}{2}} s = 50 {\displaystyle s=50} s=50So, if Ben traveled 40 mph for 2 hours, then 60 mph for another 2 hours, his average speed is 50 mph.
Given Two Speeds for Half the Distance
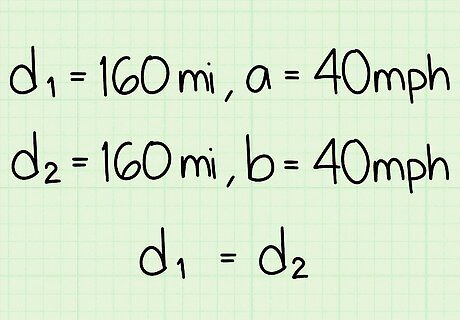
Assess what information is given. Use this method if you know: two different speeds; and that those speeds were used for the same distance. For example, if Ben drives the 160 miles to the waterpark at 40 mph, and returns the 160 miles home driving 60 mph, what is his average speed for the entire trip?
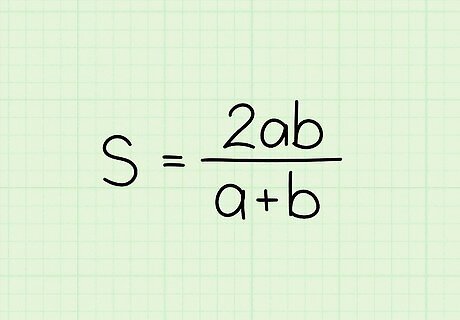
Set up the formula for average speed given two speeds used for the same distance. The formula is s = 2 a b a + b {\displaystyle s={\frac {2ab}{a+b}}} s={\frac {2ab}{a+b}}, where s {\displaystyle s} s equals the average speed, a {\displaystyle a} a equals the speed for the first half of the distance, and b {\displaystyle b} b equals the speed for the second half of the distance. Often problems requiring this method will involve a question about a return trip. In these types of problems, it doesn’t matter how far each speed is driven, as long as each speed is used for half the total distance. You can modify the formula if given three speeds for the same distance. For example, s = 3 a b c a b + b c + c a {\displaystyle s={\frac {3abc}{ab+bc+ca}}} s={\frac {3abc}{ab+bc+ca}}.
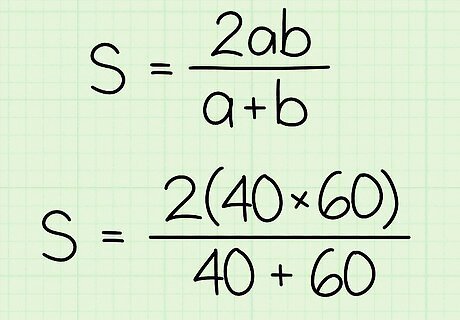
Plug the speeds into the formula. It doesn’t matter which speed you substitute for a {\displaystyle a} a and which you substitute for b {\displaystyle b} b. For example, if the first speed is 40 mph, and the second speed is 60 mph, your formula will look like this: s = ( 2 ) ( 40 ) ( 60 ) 40 + 60 {\displaystyle s={\frac {(2)(40)(60)}{40+60}}} s={\frac {(2)(40)(60)}{40+60}}.
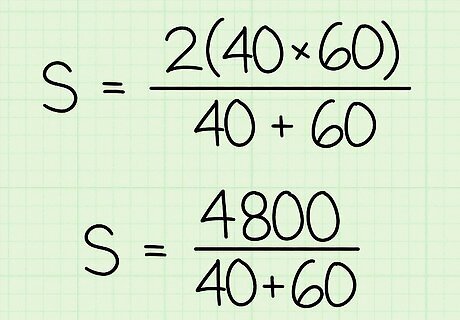
Multiply the product of the two speeds by 2. This number should be the numerator of your fraction. For example: s = ( 2 ) ( 40 ) ( 60 ) 40 + 60 {\displaystyle s={\frac {(2)(40)(60)}{40+60}}} s={\frac {(2)(40)(60)}{40+60}} s = 4800 40 + 60 {\displaystyle s={\frac {4800}{40+60}}} s={\frac {4800}{40+60}}.
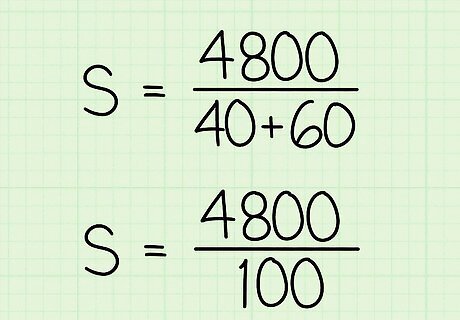
Add the two speeds together. This number should be the denominator of your fraction. For example: s = 4800 40 + 60 {\displaystyle s={\frac {4800}{40+60}}} s={\frac {4800}{40+60}} s = 4800 100 {\displaystyle s={\frac {4800}{100}}} s={\frac {4800}{100}}.

Simplify the fraction. This will give you the average speed for the entire trip. For example: s = 4800 100 {\displaystyle s={\frac {4800}{100}}} s={\frac {4800}{100}} s = 48 {\displaystyle s=48} s=48. So, if Ben drives 40 mph for 160 miles to the waterpark, then 60 mph for the 160 miles home, his average speed for the trip is 48 mph.



















Comments
0 comment