views
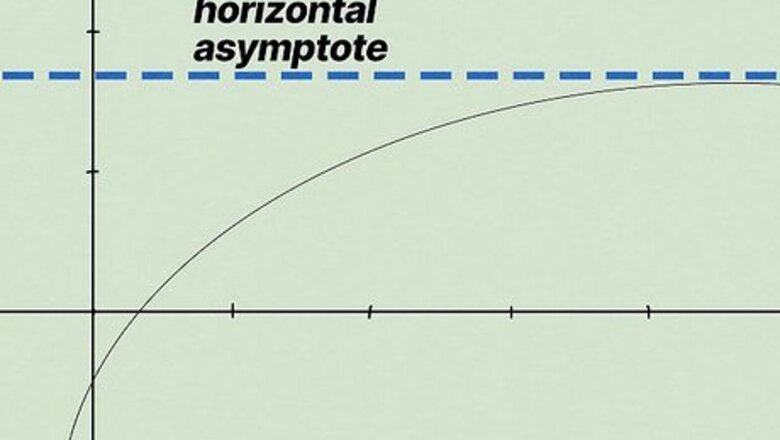
- A horizontal asymptote is the dashed horizontal line on a graph. The graphed line of the function can approach or even cross the horizontal asymptote.
- To find a horizontal asymptote, compare the degrees of the polynomials in the numerator and denominator of the rational function.
- The degree of difference between the polynomials reveals where the horizontal asymptote sits on a graph.
What is a horizontal asymptote?
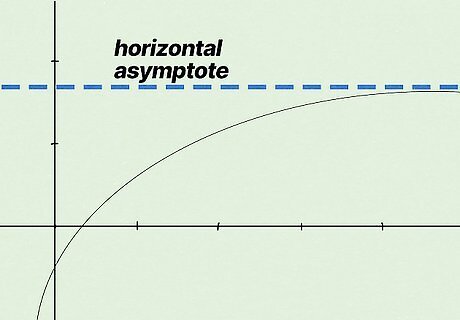
A horizontal asymptote (HA) is a line that shows the end behavior of a rational function. When you look at a graph, the HA is the horizontal dashed or dotted line. When you plot the function, the graphed line might approach or cross the HA if it becomes infinitely large or infinitely small. Horizontal asymptotes can occur on both sides of the y-axis, so don't forget to look at both sides of your graph.
How do I find a horizontal asymptote of a rational function?
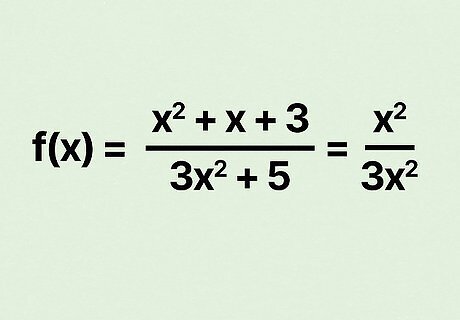
Remove all terms but the terms with the biggest exponents of x {\displaystyle x} x. Since you're not actually solving an equation, you're simply comparing the leading terms in your rational function. For example, if your equation is f ( x ) = x 2 + x + 3 3 x 2 + 5 {\displaystyle f(x)={\frac {x^{2}+x+3}{3x^{2}+5}}} {\displaystyle f(x)={\frac {x^{2}+x+3}{3x^{2}+5}}}, remove all but the leading terms to get x 2 3 x 2 {\displaystyle {\frac {x^{2}}{3x^{2}}}} {\displaystyle {\frac {x^{2}}{3x^{2}}}}. As another example, your equation might be f ( x ) = 2 + 5 x 2 + 4 x 3 x 4 + 6 {\displaystyle f(x)={\frac {2+5x^{2}+4x^{3}}{x^{4}+6}}} {\displaystyle f(x)={\frac {2+5x^{2}+4x^{3}}{x^{4}+6}}}. After you remove all but the leading terms, you'll have 4 x 3 x 4 {\displaystyle {\frac {4x^{3}}{x^{4}}}} {\displaystyle {\frac {4x^{3}}{x^{4}}}}. To give you another example, if you have f ( x ) = x 3 − 1 4 + x 2 {\displaystyle f(x)={\frac {x^{3}-1}{4+x^{2}}}} {\displaystyle f(x)={\frac {x^{3}-1}{4+x^{2}}}}, ignore the constants to get f ( x ) = x 3 x 2 {\displaystyle f(x)={\frac {x^{3}}{x^{2}}}} {\displaystyle f(x)={\frac {x^{3}}{x^{2}}}}.
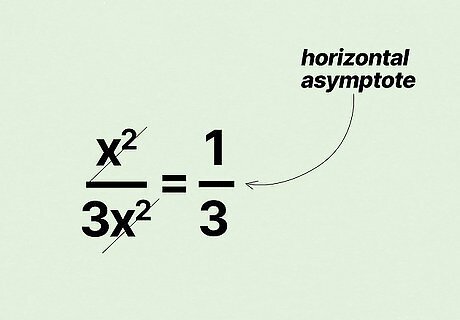
Simplify the ratio to find the horizontal asymptote for the function. Remember, you're not solving the equation—you're simplifying the leading terms in order to see the limits of the function. To go with the previous example of x 2 3 x 2 {\displaystyle {\frac {x^{2}}{3x^{2}}}} {\displaystyle {\frac {x^{2}}{3x^{2}}}}, cancel out both of the x 2 {\displaystyle {x^{2}}} {\displaystyle {x^{2}}} to get 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}}, which shows you the horizontal asymptote. For the other previous example of 4 x 3 x 4 {\displaystyle {\frac {4x^{3}}{x^{4}}}} {\displaystyle {\frac {4x^{3}}{x^{4}}}}, cancel out the top x 3 {\displaystyle {x^{3}}} {\displaystyle {x^{3}}} and take away x 3 {\displaystyle {x^{3}}} {\displaystyle {x^{3}}} from the denominator to get 4 x {\displaystyle {\frac {4}{x}}} {\displaystyle {\frac {4}{x}}} which becomes 0 {\displaystyle 0} {\displaystyle 0}. For the last example of f ( x ) = x 3 x 2 {\displaystyle f(x)={\frac {x^{3}}{x^{2}}}} {\displaystyle f(x)={\frac {x^{3}}{x^{2}}}}, remove x 2 {\displaystyle {x^{2}}} {\displaystyle {x^{2}}} from the numerator and denominator to get x {\displaystyle x} x.
Horizontal Asymptote Rules and Results
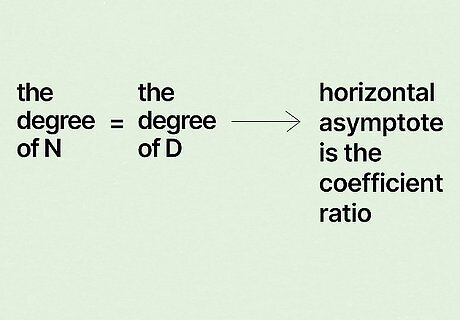
If the degree of the numerator and denominator is the same, use the coefficient ratio. If the polynomials in the numerator and denominator cancel each other out, you're left with the coefficients. Use the ratio of the coefficients to find the HA. Going back to our first example of f ( x ) = x 2 + x + 3 3 x 2 + 5 {\displaystyle f(x)={\frac {x^{2}+x+3}{3x^{2}+5}}} {\displaystyle f(x)={\frac {x^{2}+x+3}{3x^{2}+5}}}, you ended up with 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}}. In this example, the HA is 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}}.
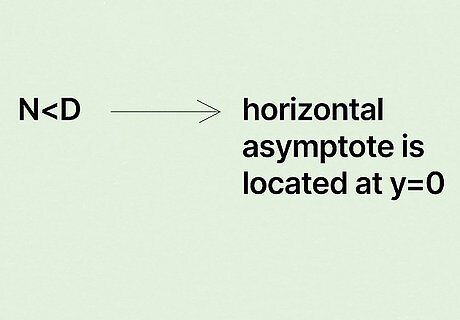
If the numerator is at a lower degree, then the HA is located at y=0. This can be put another way—N If the degree of the numerator is higher, there is no horizontal asymptote. It might help to remember this rule as N>D=no HA. When the numerator is greater than the denominator, it's not possible to have a horizontal asymptote.
In the previous example that started with
f
(
x
)
=
x
3
−
1
4
+
x
2
{\displaystyle f(x)={\frac {x^{3}-1}{4+x^{2}}}}
{\displaystyle f(x)={\frac {x^{3}-1}{4+x^{2}}}}, you were left with
x
{\displaystyle x}
x. Since
x
{\displaystyle x}
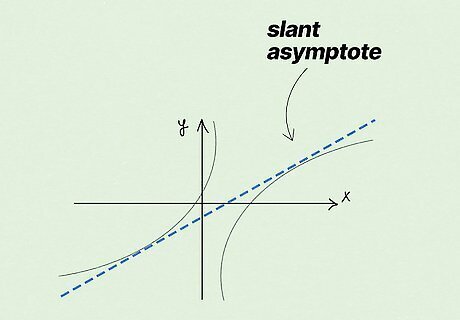
x is larger than a nonexistent denominator, no HA is possible with this equation. Horizontal asymptotes can be slanted if the degree of the numerator is greater by 1. To find a slant asymptote, perform polynomial long division. Note that as you find the slant asymptote, you'll also find the vertical asymptote.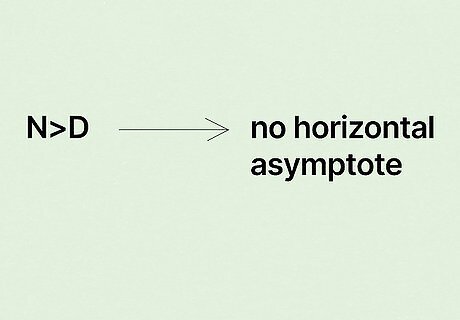
Are horizontal asymptotes the same as slant asymptotes?













Comments
0 comment