How to Calculate Bank Interest on Savings

• Learn the formula for compound interest; determine all of the variables you’ll need and plug them into the formula before crunching the numbers.
• To calculate interest with regular contributions, begin with the accumulated savings formula and input your variables before solving the equation.
• Use a spreadsheet for compounding interest; label and enter your variables before creating the equation, and use Excel’s financial functions.

Calculating Compound Interest

Know the formula for calculating the effect of compound interest. The formula for calculating compound interest accumulation on a given account balance is: A = P ( 1 + ( r n ) ) n ∗ t {\displaystyle A=P(1+({\frac {r}{n}}))^{n*t}} A=P(1+({\frac {r}{n}}))^{{n*t}}. (P) is the principal (P), (r) is the annual rate of interest, and (n) is the number of times the interest is compounded per year. (A) is the balance of the account you are calculating including the effects of interest. (t) represents the periods of time over which the interest is accumulating. It should match with the interest rate you are using (e.g. if the interest rate is an annual rate, (t) should be a number/fraction years). To determine the appropriate fraction of years for a given time period, simply divide the total number of months by 12 or divide the total number of days by 365.

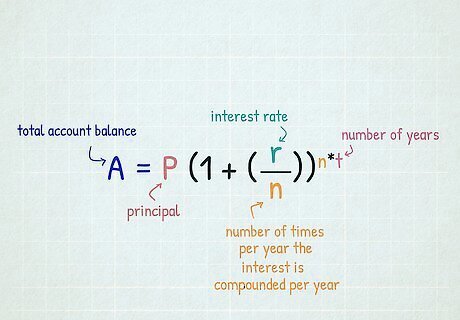
Determine the variables used in the formula. Review the terms of your personal savings account or contact a representative from your bank to fill in the equation. The principal (P) represents either the initial amount deposited into the account or the current amount that you will be measuring from for your interest calculation. The interest rate (r) should be in decimal form. A 3% interest rate should be entered as 0.03. To get this number, simply divide the stated percentage rate by 100. The value of (n) is the number of times per year the interest is calculated and added onto your balance (aka compounds). Interest most commonly compounds monthly (n=12), quarterly (n=4), or yearly (n=1) but there can be other options, depending on your specific account terms.

Plug your values into the formula. Once you have determined the amounts of each variable, insert them into the compound interest formula to determine the interest earned over the specified time scale. For example, using the values P=$1000, r=0.05 (5%), n=4 (compounded quarterly), and t=1 year, we get the following equation: A = $ 1000 ( 1 + ( 0.05 4 ) ) 4 ∗ 1 {\displaystyle A=\$1000(1+({\frac {0.05}{4}}))^{4*1}} A=\$1000(1+({\frac {0.05}{4}}))^{{4*1}}. Interest compounded daily is found in a similar way, except you would substitute 365 for the 4 used above for variable (n).

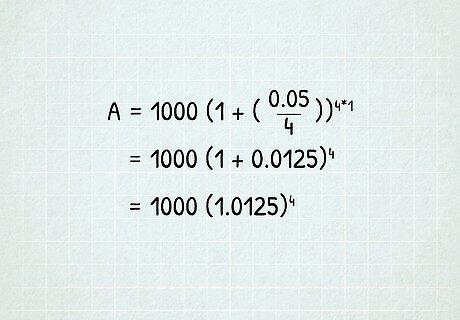
Crunch the numbers. Now that the numbers are in, it's time to solve the formula. Start by simplifying the simple parts of the equation. This includes dividing the annual rate by the number of periods to get the periodic rate (in this case 0.05 4 = 0.0125 {\displaystyle {\frac {0.05}{4}}=0.0125} {\frac {0.05}{4}}=0.0125) and solving the object n ∗ t {\displaystyle n*t} n*t which here is just 4 ∗ 1 {\displaystyle 4*1} 4*1. This will yield the following equation: A = $ 1000 ( 1 + ( 0.0125 ) ) 4 {\displaystyle A=\$1000(1+(0.0125))^{4}} A=\$1000(1+(0.0125))^{{4}}. This is then further simplified by solving for the object within the parenthesis, 1 + 0.0125 = 1.0125 {\displaystyle 1+0.0125=1.0125} 1+0.0125=1.0125. The equation will now look like this: A = $ 1000 ( 1.0125 ) 4 {\displaystyle A=\$1000(1.0125)^{4}} A=\$1000(1.0125)^{{4}}.

Solve the equation. Next, solve the exponent by raising the result of the last step to the power of four (aka 1.0125 ∗ 1.0125 ∗ 1.0125 ∗ 1.0125 {\displaystyle 1.0125*1.0125*1.0125*1.0125} 1.0125*1.0125*1.0125*1.0125). This will give you 1.051 {\displaystyle 1.051} 1.051. Your equation is now simply: A = $ 1000 ( 1.051 ) {\displaystyle A=\$1000(1.051)} A=\$1000(1.051). Multiply these two numbers together to get A = $ 1051 {\displaystyle A=\$1051} A=\$1051. This is your account value with 5% interest (compounded quarterly) after one year. Note that this is slightly higher than $ 1000 ∗ 5 % {\displaystyle \$1000*5\%} \$1000*5\% that you may have expected when the annual interest rate was quoted to you. This illustrates the importance of understanding how and when your interest compounds! The interest earned is the difference between A and P, so total interest earned = $ 1051 − $ 1000 = $ 51 {\displaystyle =\$1051-\$1000=\$51} =\$1051-\$1000=\$51.

Calculating Interest with Regular Contributions

Use the accumulated savings formula first. You can also calculate interest on an account to which you are making regular monthly contributions. This is useful if you save a certain amount each month and put that money into your savings account. The full equation is as follows: A = P ( 1 + ( r n ) ) n t + P M T ∗ ( 1 + r n ) n t − 1 r n {\displaystyle A=P(1+({\frac {r}{n}}))^{nt}+PMT*{\frac {(1+{\frac {r}{n}})^{nt}-1}{\frac {r}{n}}}} A=P(1+({\frac {r}{n}}))^{{nt}}+PMT*{\frac {(1+{\frac {r}{n}})^{{nt}}-1}{{\frac {r}{n}}}} An easy approach is to separate the compounding interest for the principal from that of the monthly contributions (or payments/PMT). To begin, calculate the interest on the principal first using the accumulated savings formula. As has been described with this formula, you can calculate the interest earned on your savings account with recurring monthly deposits and interest compounded daily, monthly or quarterly.

Use the second part of the formula to calculate the interest on your contributions. (PMT) represents your monthly contribution amount.

Identify your variables. Check your account or investment agreement to find the following variables: principal "P", the annual rate of interest "r", and the number of periods per year "n". If these variables are not readily available to you, contact your bank and ask for this information. The variable "t" represents the number of years, or portions of years, being calculated and "PMT" represents the payment/contribution made each month. The account value "A" represents the total value of the account after your chosen time period and contributions. The principal "P" represents either the balance of the account on the date that you will be starting the calculation from. The interest rate "r" represents the interest paid on the account each year. It should be expressed as a decimal in the equation. That is, a 3% interest rate should be entered as 0.03. To get this number, simply divide the stated percentage rate by 100. The value of "n" simply represents the number of times the interest is compounded each year. This should be 365 for interest compounded daily, 12 for monthly, and 4 for quarterly. Similarly, the value for "t" represents the number of years you will be calculating your future interest for. This should be either the number of years or the portion of a year if you are measuring less than a year (e.g. 0.0833 (1/12) for one month).

Input your values into the formula. Using the example of P=$1000, r=0.05 (5%), n=12 (compounded monthly), t=3 years, and PMT=$100, we get the following equation: A = $ 1000 ( 1 + ( 0.05 12 ) ) 12 ∗ 3 + $ 100 ∗ ( 1 + 0.05 12 ) 12 ∗ 3 − 1 0.05 12 {\displaystyle A=\$1000(1+({\frac {0.05}{12}}))^{12*3}+\$100*{\frac {(1+{\frac {0.05}{12}})^{12*3}-1}{\frac {0.05}{12}}}} A=\$1000(1+({\frac {0.05}{12}}))^{{12*3}}+\$100*{\frac {(1+{\frac {0.05}{12}})^{{12*3}}-1}{{\frac {0.05}{12}}}}

Simplify the equation. Begin by simplifying the object r n {\displaystyle {\frac {r}{n}}} {\frac {r}{n}} where possible by dividing the rate, 0.05, by 12. This simplifies to A = $ 1000 ( 1 + ( 0.00417 ) ) 12 ∗ 3 + $ 100 ∗ ( 1 + 0.00417 ) 12 ∗ 3 − 1 0.00417 {\displaystyle A=\$1000(1+(0.00417))^{12*3}+\$100*{\frac {(1+0.00417)^{12*3}-1}{0.00417}}} A=\$1000(1+(0.00417))^{{12*3}}+\$100*{\frac {(1+0.00417)^{{12*3}}-1}{0.00417}} You can also simplify by adding one to the rate within the parentheses. The equation will now look like this: A = $ 1000 ( 1.00417 ) ) 12 ∗ 3 + $ 100 ∗ ( 1.00417 ) 12 ∗ 3 − 1 0.00417 {\displaystyle A=\$1000(1.00417))^{12*3}+\$100*{\frac {(1.00417)^{12*3}-1}{0.00417}}} A=\$1000(1.00417))^{{12*3}}+\$100*{\frac {(1.00417)^{{12*3}}-1}{0.00417}}

Solve the exponents. First, solve the figures within the exponents, n ∗ t {\displaystyle n*t} n*t, which give 12 ∗ 3 = 36 {\displaystyle 12*3=36} 12*3=36. Then, solve the exponents to simplify the equation to A = $ 1000 ( 1.1616 ) + $ 100 ∗ 1.1616 − 1 0.00417 {\displaystyle A=\$1000(1.1616)+\$100*{\frac {1.1616-1}{0.00417}}} A=\$1000(1.1616)+\$100*{\frac {1.1616-1}{0.00417}} Simplify by subtracting the one to get A = $ 1000 ( 1.1616 ) + $ 100 ∗ 0.1616 0.00417 {\displaystyle A=\$1000(1.1616)+\$100*{\frac {0.1616}{0.00417}}} A=\$1000(1.1616)+\$100*{\frac {0.1616}{0.00417}}

Make the final calculations. Multiply the first part of the equation to get $1,161.6. Solve the second part of the equation by first dividing the numerator by the denominator of the fraction to get 0.1616 0.00417 = 38.753 {\displaystyle {\frac {0.1616}{0.00417}}=38.753} {\frac {0.1616}{0.00417}}=38.753. Multiply this number by the value of the payment (in this case $100) to get the second part of the equation. Our equation is now: A = $ 1161.6 + $ 3875.30 = $ 5 , 036.9 {\displaystyle A=\$1161.6+\$3875.30=\$5,036.9} {\displaystyle A=\$1161.6+\$3875.30=\$5,036.9}. The account value under these conditions would be $ 5 , 036.9 {\displaystyle \$5,036.9} {\displaystyle \$5,036.9}.

Calculate your total interest earned. In this equation, actual interest earned would be the total amount (A) minus the principal (P) and the number of payments times the payment amount (PMT*n*t). So, in the example, I n t e r e s t = $ 5036.9 − $ 1000 − $ 100 ( 12 ∗ 3 ) {\displaystyle Interest=\$5036.9-\$1000-\$100(12*3)} {\displaystyle Interest=\$5036.9-\$1000-\$100(12*3)} and then $ 5036.9 − $ 1000 − $ 3600 = $ 436.81 {\displaystyle \$5036.9-\$1000-\$3600=\$436.81} {\displaystyle \$5036.9-\$1000-\$3600=\$436.81}.

Using a Spreadsheet to Calculate Compounding Interest

Open a new spreadsheet. Excel and other similar spreadsheet programs (e.g. Google Sheets) allow you to save time on the math behind these calculations and even offer shortcuts in the form of built-in financial functions to help you calculate compounding interest.

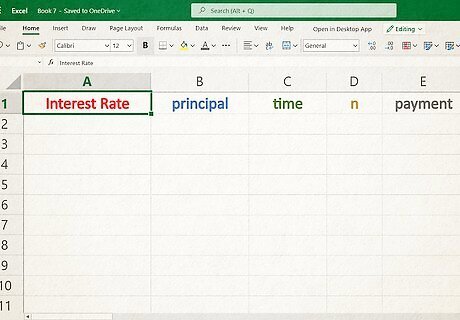
Label your variables. When using a spreadsheet, it's always helpful to be as organized and clear as possible. Start by labeling a column of cells with the key information you'll be using in your calculation (e.g. interest rate, principal, time, n, payment).

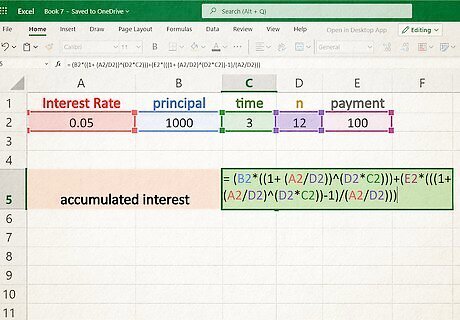
Type in your variables. Now fill out the data you have about your specific account in the next column over. This not only makes the the spreadsheet easier to read and interpret later, it also leaves room for you to change one or more of your variables later on in order to look at different possible savings scenarios.

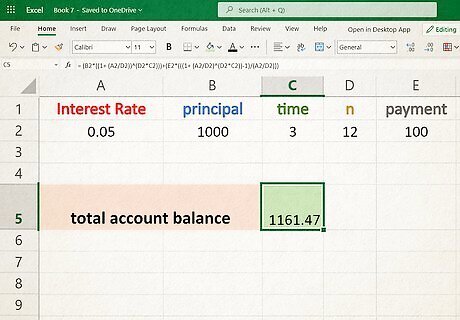
Create your equation. The next step is to type in your own version of the accumulated interest equation ( A = P ( 1 + ( r n ) ) n ∗ t {\displaystyle A=P(1+({\frac {r}{n}}))^{n*t}} A=P(1+({\frac {r}{n}}))^{{n*t}} ) or the extended version which takes into account your regular monthly contributions to the account ( A = P ( 1 + ( r n ) ) n t + P M T ∗ ( 1 + r n ) n t − 1 r n {\displaystyle A=P(1+({\frac {r}{n}}))^{nt}+PMT*{\frac {(1+{\frac {r}{n}})^{nt}-1}{\frac {r}{n}}}} A=P(1+({\frac {r}{n}}))^{{nt}}+PMT*{\frac {(1+{\frac {r}{n}})^{{nt}}-1}{{\frac {r}{n}}}} ). Use any blank cell, begin with an "=", and use normal math conventions (parentheses as necessary) to type the appropriate equation. Instead of entering variables like (P) and (n), type in the corresponding cell names where you have stored those data values or else simply click the appropriate cell while editing your equation.

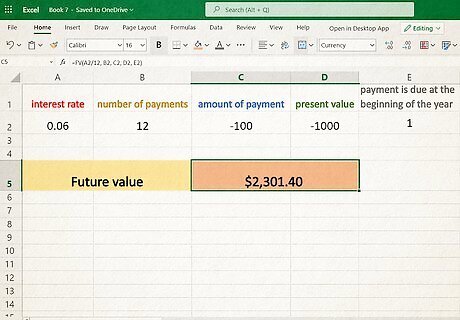
Use financial functions. Excel also offers certain financial functions that may help your calculation. Specifically, "future value" (FV) may be of use because it calculates the value of an account at some point in the future given the same set of variables you've now become accustomed to. To access this function go to any blank cell and type "=FV(". Excel should then bring up a guidance window as soon as you open the function parenthesis in order to help you insert the appropriate parameters into your function. The future value function is designed with paying an account balance down as it continues to accumulate interest instead of with accumulating savings account interest. Because of this it automatically yields a negative number. Counteract this issue by typing = − 1 ∗ F V ( {\displaystyle =-1*FV(} =-1*FV( The FV function takes similar data parameters separated by commas but not exactly the same ones. For instance, "rate" refers to r / n {\displaystyle r/n} r/n (the annual interest rate divided by "n"). This will calculate automatically from within the FV function's parenthesis. The parameter "nper" refers to the variable n ∗ t {\displaystyle n*t} n*t - the total number of periods over which interest is accumulating and the total number of payments. In other words, if your PMT is not 0, the FV function will assume you are contributing the PMT amount across each and every period as defined by "nper". Note that this function is most often used for (things like) calculating how a mortgage principal is paid down over time by regular payments. For instance if you plan to contribute every month for 5 years, "nper" would be 60 (5 years * 12 months). PMT is your regular contribution amount over the entire period (one contribution per "n") "[pv]" (aka Present Value) is the principal amount - your account's starting balance. The final variable, "[type]" can be left blank for this calculation (when it is the function sets it automatically to 0). The FV function allows for you to do basic calculations within the function parameters, for instance the completed FV function could look like − 1 ∗ F V ( .05 / 12 , 12 , 100 , 5000 ) {\displaystyle -1*FV(.05/12,12,100,5000)} -1*FV(.05/12,12,100,5000). This would signify a 5% annual interest rate which compounded monthly for 12 months, over which time you contribute $100/month and your starting (principal) balance is $5000. The answer to this function will tell you the account balance after 1 year ($6483.70).