
views
- The main difference is that the t test is used when population variance is unknown.
- Calculate the z statistic using the formula
- Calculate the t statistic using
Key Differences
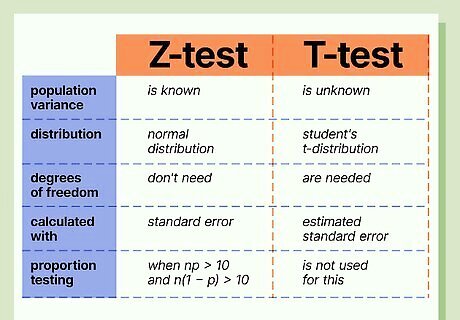
Take a look at these key differences between the z test and t test. We don’t know the population variance in t testing, while we do know it in z testing. The z test uses a normal distribution while the t test uses the Student's t distribution. Degrees of freedom are needed in t testing, not in z testing. The z statistic is calculated with the standard error. The t statistic uses the estimated standard error. The z test is used for testing proportions when np > 10 and n(1 - p) > 10. The t test is not used for proportion testing.
Z Test

Use the z statistic to carry out hypothesis testing. The z statistic uses a sampling distribution. Then, it turns it into a standard normal distribution. To calculate the z statistic, use this formula: z = M − m u s i g m a M {\displaystyle z={\frac {M-mu}{sigma_{M}}}} {\displaystyle z={\frac {M-mu}{sigma_{M}}}} s i g m a M = s i g m a n {\displaystyle sigma_{M}={\frac {sigma}{\sqrt {n}}}} {\displaystyle sigma_{M}={\frac {sigma}{\sqrt {n}}}} where M {\displaystyle M} M is the sample mean m u {\displaystyle mu} {\displaystyle mu} is the population mean s i g m a M {\displaystyle sigma_{M}} {\displaystyle sigma_{M}} is the sample standard error s i g m a {\displaystyle sigma} {\displaystyle sigma} is the population standard deviation n {\displaystyle n} n is the sample size
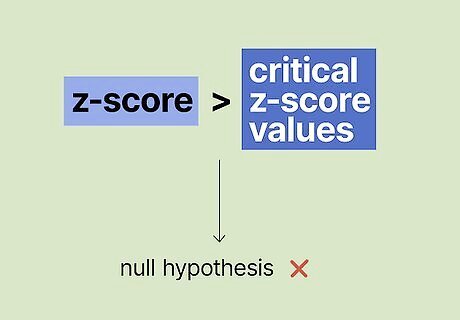
Make a decision. If the calculated z statistic (also called z score) is greater than the critical z value, you reject the null hypothesis and have significant evidence supporting the alternative hypothesis. If you’re testing a proportion, check out our guide on performing hypothesis testing for a proportion.
T Test

Use the t statistic to carry out hypothesis testing. The t statistic uses a sampling distribution. Then, it turns it into the t distribution. To calculate the t statistic, use this formula: t = M − m u s M {\displaystyle t={\frac {M-mu}{s_{M}}}} {\displaystyle t={\frac {M-mu}{s_{M}}}} s M = S D n {\displaystyle s_{M}={\frac {SD}{\sqrt {n}}}} {\displaystyle s_{M}={\frac {SD}{\sqrt {n}}}} where M {\displaystyle M} M is the sample mean m u {\displaystyle mu} {\displaystyle mu} is the population mean s M {\displaystyle s_{M}} {\displaystyle s_{M}} is the estimated standard error S D {\displaystyle SD} {\displaystyle SD} is the sample standard deviation n {\displaystyle n} n is the sample size
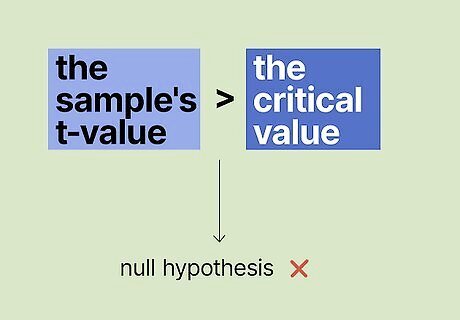
Make a decision. If the calculated z statistic is greater than the critical z value, you reject the null hypothesis and have significant evidence supporting the alternative hypothesis. We cover two-sample t tests in this guide.
Z Test Example

Check out this example of a z test problem. Our population of interest is students who have taken College Class 101 with Dr. Professor. We know that all of Dr. Professor’s past students have averaged 85% on the final, with a standard deviation of 5%. Now we’re interested in seeing if Dr. Professor’s most recent class of 25 students has done significantly better than all her previous classes. The average on the final this year was an 87%, with a standard deviation of 4%.

Set up the hypothesis. null hypothesis: M <= m u {\displaystyle M<=mu} {\displaystyle M alternative hypothesis: M > m u {\displaystyle M>mu} {\displaystyle M>mu} a l p h a = 0.05 {\displaystyle alpha=0.05} {\displaystyle alpha=0.05}

Calculate the sample standard error. s i g m a M = s i g m a n {\displaystyle sigma_{M}={\frac {sigma}{\sqrt {n}}}} {\displaystyle sigma_{M}={\frac {sigma}{\sqrt {n}}}} s i g m a M = 5 25 {\displaystyle sigma_{M}={\frac {5}{\sqrt {25}}}} {\displaystyle sigma_{M}={\frac {5}{\sqrt {25}}}} s i g m a M = 1 {\displaystyle sigma_{M}=1} {\displaystyle sigma_{M}=1}

Calculate the z statistic. z = M − m u s i g m a M {\displaystyle z={\frac {M-mu}{sigma_{M}}}} {\displaystyle z={\frac {M-mu}{sigma_{M}}}} z = 87 − 85 1 {\displaystyle z={\frac {87-85}{1}}} {\displaystyle z={\frac {87-85}{1}}} z = 2 {\displaystyle z=2} {\displaystyle z=2}
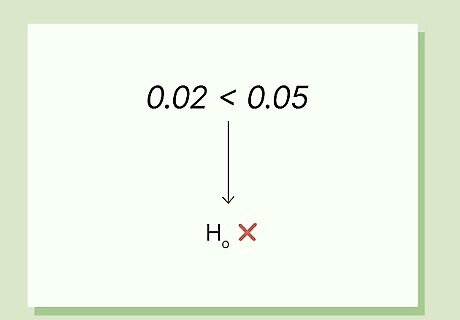
Find the p-value and interpret the results. Using a z table or an online z calculator, you can find that a z statistic of 2 corresponds with a p-value of about 0.02. Because the p-value is smaller than our alpha of 0.05, we have evidence to reject the null hypothesis that the recent class’s improved exam scores are due to chance alone.
T Test Example

Check out this example of a t test problem. This time we’re comparing the final exam grades of Dr. Professor’s most recent class to the average final exam grade of all students in the school. She wants to know if her students scored significantly higher than the average. We don’t know the standard deviation of all the student’s exam scores. Dr. Professor’s class of 25 students averaged 87% with a standard deviation of 4%, and the school-wide average final exam score was 79%.

Set up the hypothesis. null hypothesis: M <= m u {\displaystyle M<=mu} {\displaystyle M alternative hypothesis: M > m u {\displaystyle M>mu} {\displaystyle M>mu} a l p h a = 0.05 {\displaystyle alpha=0.05} {\displaystyle alpha=0.05}

Calculate the estimated standard error. s M = S D n {\displaystyle s_{M}={\frac {SD}{\sqrt {n}}}} {\displaystyle s_{M}={\frac {SD}{\sqrt {n}}}} s M = 4 25 {\displaystyle s_{M}={\frac {4}{\sqrt {25}}}} {\displaystyle s_{M}={\frac {4}{\sqrt {25}}}} s M = 0.8 {\displaystyle s_{M}=0.8} {\displaystyle s_{M}=0.8}

Calculate the t statistic. t = M − m u s M {\displaystyle t={\frac {M-mu}{s_{M}}}} {\displaystyle t={\frac {M-mu}{s_{M}}}} t = 87 − 79 0.8 {\displaystyle t={\frac {87-79}{0.8}}} {\displaystyle t={\frac {87-79}{0.8}}} t = 10 {\displaystyle t=10} t=10
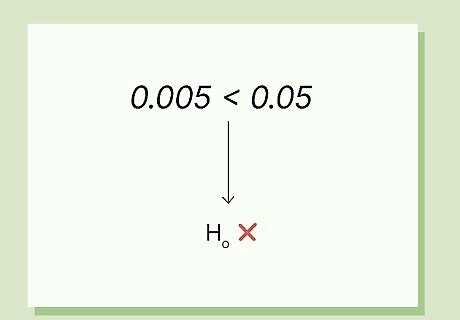
Find the p-value and interpret the results. Using a t table or an online calculator, you can find that a t statistic of 10, with 24 degrees of freedom, corresponds with a p-value of less than .005, which means we have evidence to reject the null hypothesis that Dr. Professor’s class’s final exam score average is no higher than the school-wide average.


















Comments
0 comment