views
Figuring out the Answer (Hints)
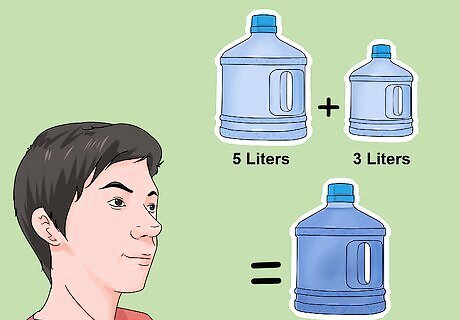
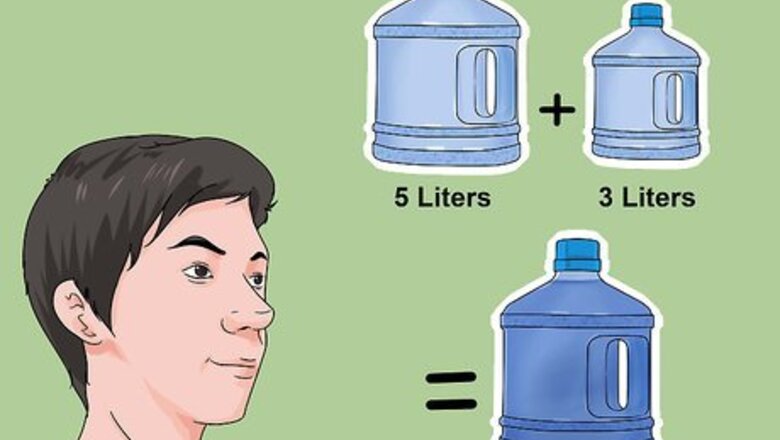
Simplify the question and your options. Setting the movie aside for the moment, think of the riddle in its most basic terms. What do you know, what's your goal, and what are your options? A simpler way to look at the riddle might be: You have two empty water jugs in your hands. One holds 3 gallons of water, the other holds 5 gallons of water. You need to use these two jugs to measure exactly 4 gallons of water. You have an unlimited amount of water to do so.

Determine where you will keep the 4 gallons of water. In order to measure out your 4 gallons, you need to put it somewhere. As John McClane rightly deduces, you couldn't possibly fit it in the 3-gallon jug, which means the right answer must involve getting the right amount of water in the 5-gallon jug.
Know that, like all good riddles, you have everything you need for a solution. The solution does not involve bringing in another jug, or eyeballing the water levels perfectly, or finding fractions of jugs. You have two jugs and an unlimited supply of water. How can you use just those things to get to 4 gallons? More specifically, how can you use 3 and 5 to get to 4? Unlimited water means you can use or pour out as much as you want. You are not able to guess exactly how much water is in the jug unless you fill it all the way up.

Realize that this is, at heart, a simple math problem. Ignore the water and the jugs for a moment if you are still stuck. How can you add or subtract 3's and 5's to get to 4? This is really all you are doing; the numbers just happen to represent gallons. Adding water or dumping it out is really just addition and subtraction.
Getting the Solution (Correct Answers)
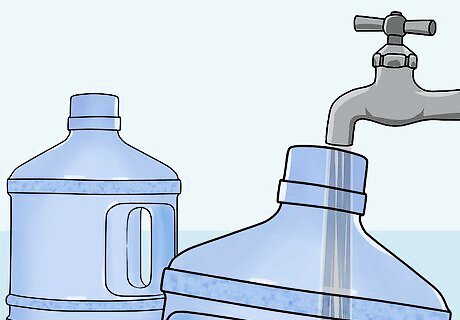
Fill the 5-jug up completely. There will be, of course, 5 gallons in the 5-jug. You must fill all the gallons up to the top, otherwise you don't actually know how much you have.
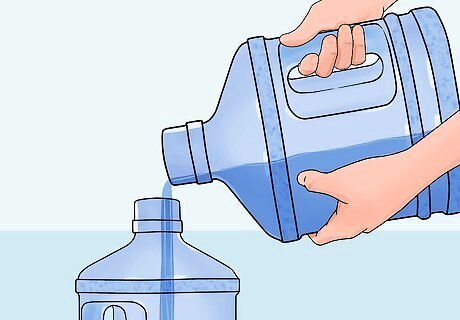
Use the water from the 5-jug to fill up the 3-jug. You're left with 3 gallons in the 3-jug and 2 gallons in the 5-jug.

Pour out the 3-gallon jug. You're left with nothing in the 3-jug and 2 gallons in the 5-jug.
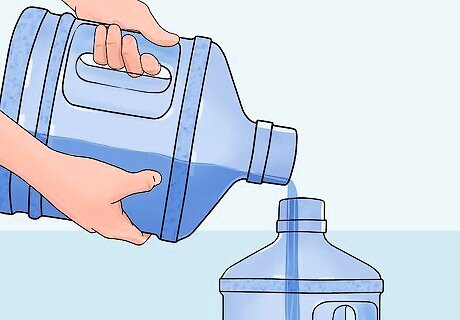
Transfer the water from the 5-jug to the three jug. You're left with 2 gallons in the 3-jug. And nothing in the 5-jug.

Fill up the 5-jug completely. You now have 2 gallons in the 3-jug and 5 in the 5-jug. This means that there is 1 gallon (3.8 L) of space left in the 3-jug.

Use the water from the 5-jug to fill up the 3-jug. Fill up the last gallon of space in the 3-jug with the water from the 5-jug. This leaves you with 3 gallons in the 3-jug, and 4 gallons in the 5-jug.
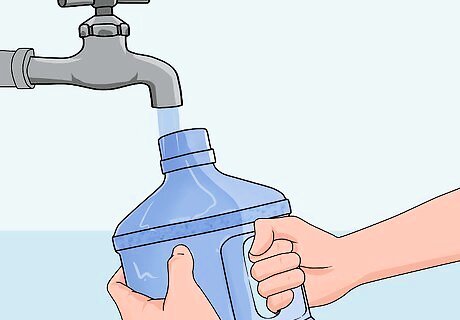
Fill the 3-jug completely with water. You now have 3 gallons (11.4 L) of water.

Transfer this water into the 5-jug. You now have nothing in the 3-jug, and 3 gallons (11.4 L) in the 5-jug.

Re-fill the 3-jug with water. You now have 3 gallons (11.4 L) in the 3-jug and 3 gallons in the 5-jug.
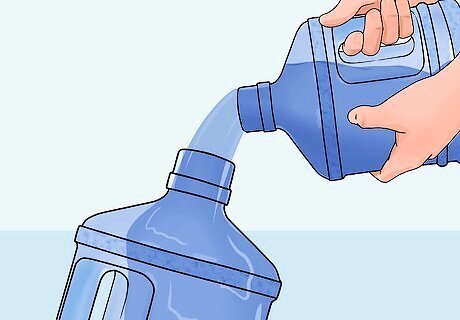
Fill the 5-jug with water from your 3-jug. You now have 1 gallon (3.8 L) in the 3-jug and 5 gallons (18.9 L) in the 5-jug. This is because, in the last step, you only had 2 gallons (7.6 L) of space left over, so you could only pour 2 gallons.

Pour out the 5-jug and refill it with your 1 gallon. You now have nothing in the 3-jug and 1 gallon in the 5-jug

Fill up the 3-jug. You now have 3 gallons (11.4 L) in the 3-jug and 1 in the 5-jug.

Transfer the 3 gallons (11.4 L) of water into the 5-jug to end up with 4 gallons (15.1 L). Simply pour over your three gallons into the 5-jug, which only had 1 gallon (3.8 L) in it previously. 1+3=4, and a successfully defused bomb.


















Comments
0 comment