How to Find the Surface Area of a Rectangular Prism

Finding the Surface Area

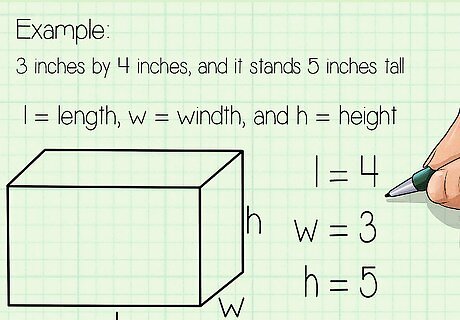
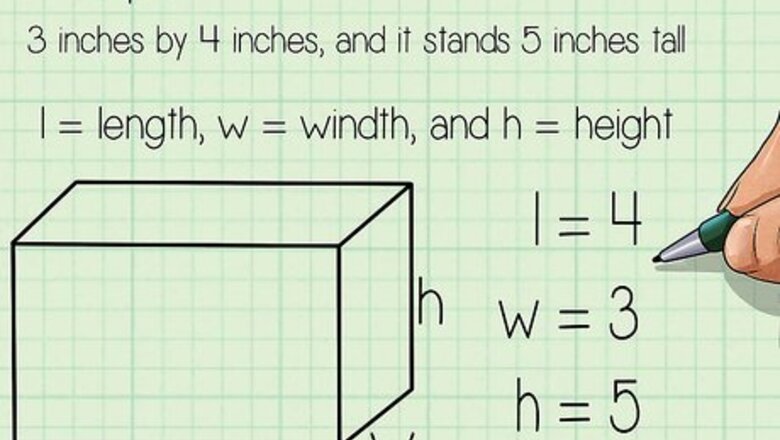
Label the length, width, and height of your rectangular prism. Each rectangular prism has a length, a width, and a height. Draw a picture of the prism, and write the symbols l, w, and h next to three different edges of the shape. If you're not sure which sides to label, pick any corner. Label the three lines that meet at that corner. For example: A box has a base that measures 3 inches by 4 inches, and it stands 5 inches tall. The long side of the base is 4 inches, so l = 4, w = 3, and h = 5.

Look at the six faces of the prism. To cover the whole surface area, you'd need to paint six different "faces." Think about each one — or find a box of cereal and look at them directly: There are a top and bottom face. Both are the same size. There are a front and a back face. Both are the same size. There are a left and right face. Both are the same size. If you have trouble picturing this, cut a box apart along the edges and lay it out.

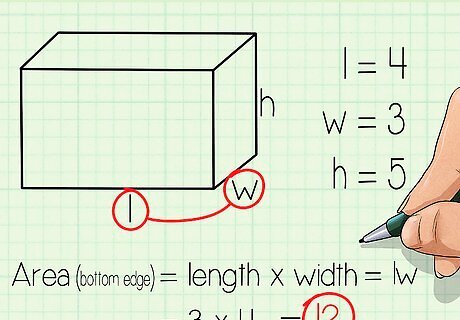
Find the area of the bottom face. To start out, let's find the surface area of just one face: the bottom. This is a rectangle, just like every face. One edge of the rectangle is labeled length and the other is labeled width. To find the area of the rectangle, just multiply the two edges together. Area (bottom edge) = length times width = lw. Going back to our example, the area of the bottom face is 4 inches x 3 inches = 12 square inches.

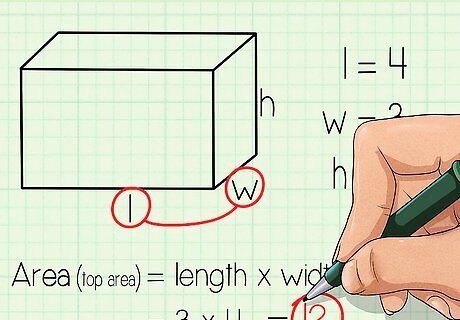
Find the area of the top face. Wait a second — we already noticed that the top and bottom faces are the same size. This must also have an area of lw. In our example, the top area is also 12 square inches.

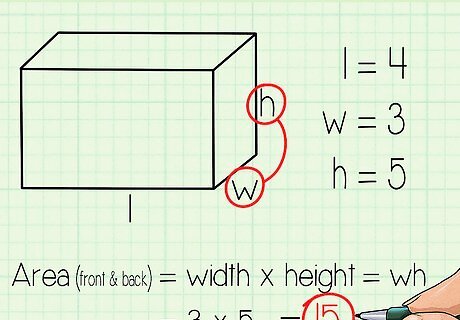
Find the area of the front and back faces. Go back to your diagram and look at the front face: the one with one edge labeled width and one labeled height. The area of the front face = width times height = wh. The area of the back is also wh. In our example, w = 3 inches and h = 5 inches, so the area of the front is 3 inches x 5 inches =15 square inches. The area of the back face is also 15 square inches.

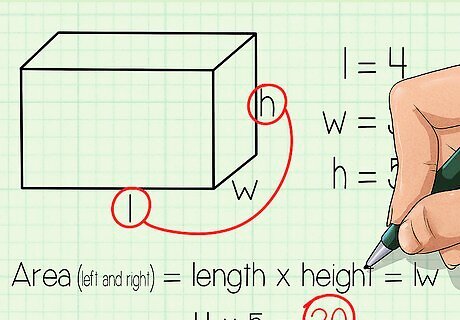
Find the area of the left and right faces. We've just got two faces left, each the same size. One edge is the length of the prism, and one edge is the height of the prism. The area of the left face is lh and the area of the right face is also lh. In our example, l = 4 inches and h = 5 inches, so the area of the left face = 4 inches x 5 inches = 20 square inches. The area of the right face is also 20 square inches.

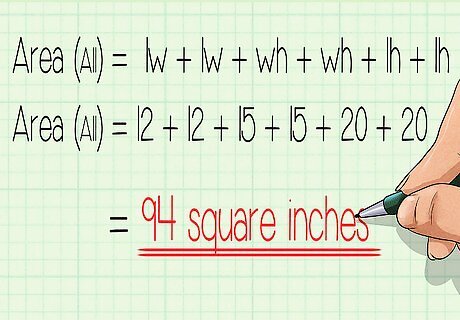
Add the six areas together. Now you've found the area of each of the six faces. Add them all together to get the area of the whole shape: lw + lw + wh + wh + lh + lh. You can use this formula for any rectangular prism, and you will always get the surface area. To finish our example, just add up all the blue numbers above: 12 + 12 + 15 + 15 + 20 + 20 = 94 square inches.

Making the Formula Shorter

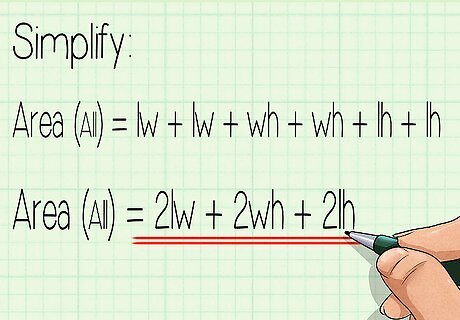
Simplify the formula. You now know enough to find the surface area of any rectangular prism. You can do it faster if you've learned some basic algebra. Start with our equation above: Area of a rectangular prism = lw + lw + wh + wh + lh + lh. If we combine all the terms that are the same, we get: Area of a rectangular prism = 2lw + 2wh + 2lh

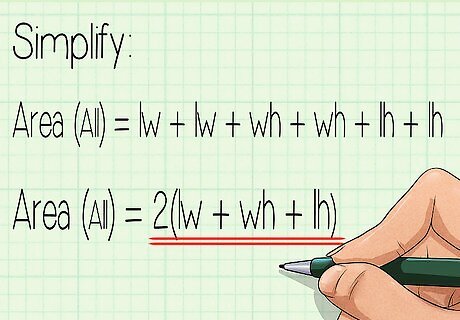
Factor out the two. If you know how to factor in algebra, you can make it even shorter: Area of a Rectangular Prism = 2lw + 2wh + 2lh = 2(lw + wh + lh).

Test it on an example. Let's go back to our example box, with length 4, width 3, and height 5. Plug these numbers into the formula: Area = 2(lw + wh + lh) = 2 x (lw + wh + lh) = 2 x (4x3 + 3x5 + 4x5) = 2 x (12 + 15 + 20) = 2 x (47) = 94 square inches. That's the same answer we got before. Once you've practiced doing these equations, this is a much faster way to find the surface area.