
views
A
{\displaystyle A}
is the set of vectors that satisfy the homogeneous equation
A
x
=
0.
{\displaystyle A\mathbf {x} =0.}
Unlike the column space
Col
A
,
{\displaystyle \operatorname {Col} A,}
it is not immediately obvious what the relationship is between the columns of
A
{\displaystyle A}
and
Nul
A
.
{\displaystyle \operatorname {Nul} A.}
Every matrix has a trivial null space - the zero vector. This article will demonstrate how to find non-trivial null spaces.

Consider a matrix A {\displaystyle A} A with dimensions of m × n {\displaystyle m\times n} m\times n. Below, your matrix is 3 × 5. {\displaystyle 3\times 5.} 3\times 5. A = ( − 3 6 − 1 1 − 7 1 − 2 2 3 − 1 2 − 4 5 8 − 4 ) {\displaystyle A={\begin{pmatrix}-3&6&-1&1&-7\\1&-2&2&3&-1\\2&-4&5&8&-4\end{pmatrix}}} A={\begin{pmatrix}-3&6&-1&1&-7\\1&-2&2&3&-1\\2&-4&5&8&-4\end{pmatrix}}

Row-reduce to reduced row-echelon form (RREF). For large matrices, you can usually use a calculator. Recognize that row-reduction here does not change the augment of the matrix because the augment is 0. ( 1 − 2 0 − 1 3 0 0 1 2 − 2 0 0 0 0 0 ) {\displaystyle {\begin{pmatrix}1&-2&0&-1&3\\0&0&1&2&-2\\0&0&0&0&0\end{pmatrix}}} {\begin{pmatrix}1&-2&0&-1&3\\0&0&1&2&-2\\0&0&0&0&0\end{pmatrix}} We can clearly see that the pivots - the leading coefficients - rest in columns 1 and 3. That means that x 1 {\displaystyle x_{1}} x_{{1}} and x 3 {\displaystyle x_{3}} x_{{3}} have their identifying equations. The result is that x 2 , x 4 , x 5 {\displaystyle x_{2},x_{4},x_{5}} x_{{2}},x_{{4}},x_{{5}} are all free variables.

Write out the RREF matrix in equation form. x 1 − 2 x 2 − x 4 + 3 x 5 = 0 x 3 + 2 x 4 − 2 x 5 = 0 {\displaystyle {\begin{aligned}x_{1}-2x_{2}-x_{4}+3x_{5}&=0\\x_{3}+2x_{4}-2x_{5}&=0\end{aligned}}} {\begin{aligned}x_{{1}}-2x_{{2}}-x_{{4}}+3x_{{5}}&=0\\x_{{3}}+2x_{{4}}-2x_{{5}}&=0\end{aligned}}
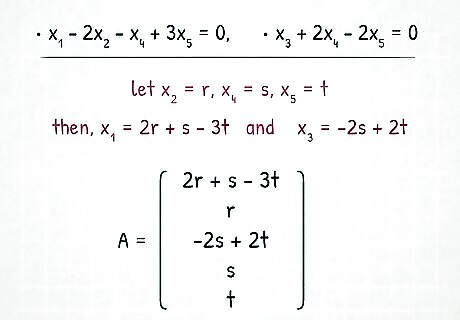
Reparameterize the free variables and solve. Let x 2 = r , x 4 = s , x 5 = t . {\displaystyle x_{2}=r,x_{4}=s,x_{5}=t.} x_{{2}}=r,x_{{4}}=s,x_{{5}}=t. Then x 1 = 2 r + s − 3 t {\displaystyle x_{1}=2r+s-3t} x_{{1}}=2r+s-3t and x 3 = − 2 s + 2 t . {\displaystyle x_{3}=-2s+2t.} x_{{3}}=-2s+2t. x = ( 2 r + s − 3 t r − 2 s + 2 t s t ) {\displaystyle \mathbf {x} ={\begin{pmatrix}2r+s-3t\\r\\-2s+2t\\s\\t\end{pmatrix}}} {\mathbf {x}}={\begin{pmatrix}2r+s-3t\\r\\-2s+2t\\s\\t\end{pmatrix}}

Rewrite the solution as a linear combination of vectors. The weights will be the free variables. Because they can be anything, you can write the solution as a span. Nul A = Span { ( 2 1 0 0 0 ) , ( 1 0 − 2 1 0 ) , ( − 3 0 2 0 1 ) } {\displaystyle \operatorname {Nul} A=\operatorname {Span} \left\{{\begin{pmatrix}2\\1\\0\\0\\0\end{pmatrix}},{\begin{pmatrix}1\\0\\-2\\1\\0\end{pmatrix}},{\begin{pmatrix}-3\\0\\2\\0\\1\end{pmatrix}}\right\}} \operatorname {Nul}A=\operatorname {Span}\left\{{\begin{pmatrix}2\\1\\0\\0\\0\end{pmatrix}},{\begin{pmatrix}1\\0\\-2\\1\\0\end{pmatrix}},{\begin{pmatrix}-3\\0\\2\\0\\1\end{pmatrix}}\right\} This null space is said to have dimension 3, for there are three basis vectors in this set, and is a subset of R 5 , {\displaystyle \mathbb {R} ^{5},} {\mathbb {R}}^{{5}}, for the number of entries in each vector. Notice that the basis vectors do not have much in common with the rows of A {\displaystyle A} A at first, but a quick check by taking the inner product of any of the rows of A {\displaystyle A} A with any of the basis vectors of Nul A {\displaystyle \operatorname {Nul} A} \operatorname {Nul}A confirms that they are orthogonal.



















Comments
0 comment