views
- Use the Arrhenius equation as your starting point for calculating activation energy: k = Ae^(-E_a/RT).
- Rearrange the equation to E_a = -R * T * ln(k/A) if you’re given one temperature reading and the pre-exponential factor.
- Adjust the equation to E_a = R * ln(k_1/k_2) / (1/T_2 - 1/T_1) if you’re given two temperature readings and two rate constant amounts.
What is activation energy?
It’s the minimum amount of energy required to begin a chemical reaction. It is, you might say, the energy “barrier” that needs to be broken through, or the energy “hump” that needs to be passed over, in order for the reactants’ existing bonds to break and begin forming new bonds. If this minimum threshold isn’t met, the reaction won’t happen. Swedish scientist Svante Arrhenius pioneered the concept of activation energy and, in 1889, came up with an equation to calculate it. This is now known as the “Arrhenius equation:" k = Ae^(-E_a/RT)
Sample Problem (Type 1)
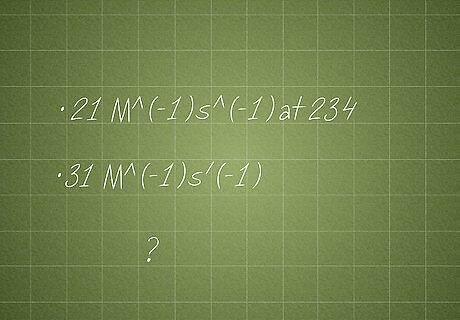
If the rate constant is 21 M^(-1)s^(-1) at 234 K and the pre-exponential factor is 31 M^(-1)s^(-1), what is the activation energy? This type of question provides you with the pre-exponential factor (or frequency factor), which means you can calculate the activation energy at a single temperature value. (The other common type of activation energy question provides you with two temperature values, but not the pre-exponential factor.) The pre-exponential factor is a temperature-dependent representation of the frequency of molecular collisions.
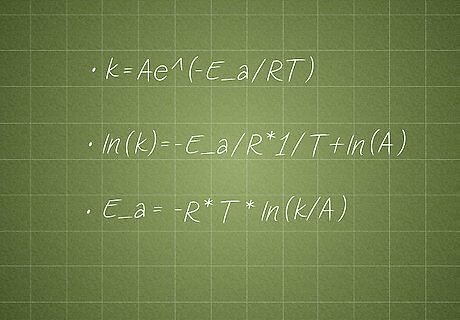
Rearrange the Arrhenius equation to solve for E_a. In the Arrhenius equation [k = Ae^(-E_a/RT)], E_a represents the activation energy, k is the rate constant, A is the pre-exponential factor, R is the ideal gas constant (8.3145), T is the temperature (in Kelvins), and e is the exponential constant (2.718). You can rearrange the equation to solve for the activation energy as follows: k = Ae^(-E_a/RT) ln(k) = -E_a/R * 1/T + ln(A) E_a = -R * T * ln(k/A)
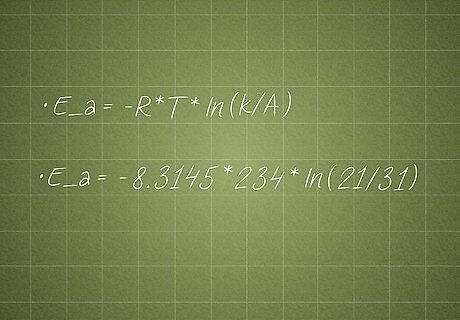
Input the given data into the rearranged equation. The question gave you the temperature (234 K), the rate constant (21), and the pre-exponential factor (31), so plug these into the correct spots: E_a = -R * T * ln(k/A) E_a = -8.3145 * 234 * ln(21/31)
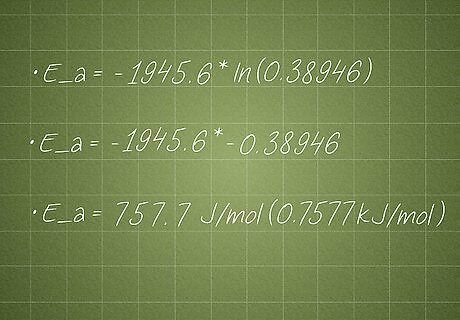
Solve the equation. Grab a scientific calculator (or an online version) and use it to determine the activation energy (given in J/mol, or, in some cases, kJ/mol, which is just J/mol divided by 1000). E_a = -1945.6 * ln(0.38946) E_a = -1945.6 * -0.38946 E_a = 757.7 J/mol (0.7577 kJ/mol)
Sample Problem (Type 2)
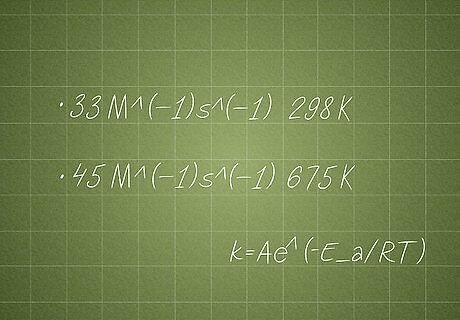
What is the activation energy of a reaction if the rate constant is 33 M^(-1)s^(-1) at 298 K and 45 M^(-1)s^(-1) at 675 K? This form of question omits the pre-exponential factor but provides two temperature readings (and two rate constants). You’ll still get the answer by using the Arrhenius equation—just rearranged differently. As a refresher, the original Arrhenius equation is k = Ae^(-E_a/RT).
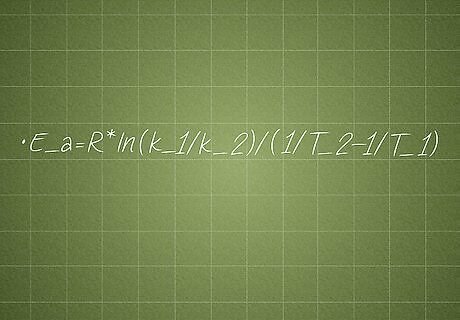
Use the equation form for multiple temperatures and constants. Without going into extensive detail here, let’s just say that the original Arrhenius equation can be rearranged into the following form: ln(k_1/k_2) = -E_a/R * (1/T_2 - 1/T_1). (Remember that k represents the rate constant, T the temperature, R the ideal gas constant, and E_a the activation energy.) This can be further rearranged to solve for the activation energy: E_a = R * ln(k_1/k_2) / (1/T_2 - 1/T_1)

Plug in the given data. The first given rate constant and temperature are k_1 and T_1, while the second are k_2 and T_2: E_a = R * ln(k_1/k_2) / (1/T_2 - 1/T_1) E_a = 8.3145 * ln(33/45) / (1/675 - 1/298)

Solve for E_a to get the result in J/mol. If you’re asked to provide the answer in kJ/mol, simply divide by 1000. E_a = 8.3145 * ln(33/45) / (1/675 - 1/298) E_a = 8.3145 * ln(0.73333) / (0.0014814 - 0.0033557) E_a = 8.3145 * -0.31016 / -0.0018743 E_a = 1375.9 J/mol
More Examples
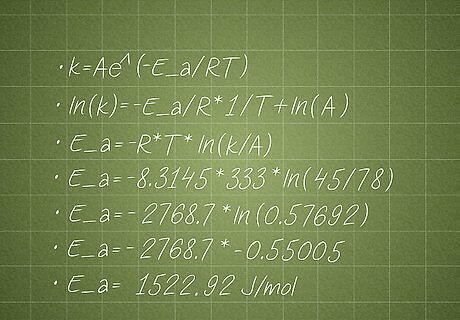
If the rate constant is 45 M^(-1)s^(-1) at 333 K and the pre-exponential factor is 78 M^(-1)s^(-1), what is the activation energy? k = Ae^(-E_a/RT) ln(k) = -E_a/R * 1/T + ln(A) E_a = -R * T * ln(k/A) E_a = -8.3145 * 333 * ln(45/78) E_a = -2768.7 * ln(0.57692) E_a = -2768.7 * -0.55005 E_a = 1522.92 J/mol
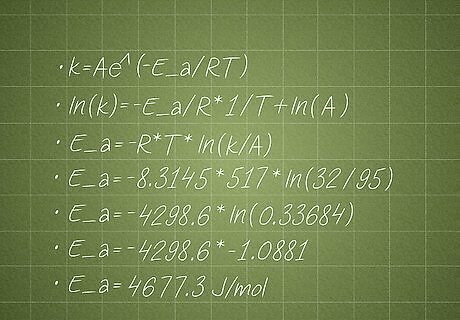
If the rate constant is 32 M^(-1)s^(-1) at 517 K and the pre-exponential factor is 95 M^(-1)s^(-1), what is the activation energy? k = Ae^(-E_a/RT) ln(k) = -E_a/R * 1/T + ln(A) E_a = -R * T * ln(k/A) E_a = -8.3145 * 517 * ln(32/95) E_a = -4298.6 * ln(0.33684) E_a = -4298.6 * -1.0881 E_a = 4677.3 J/mol

What is the activation energy of a reaction if the rate constant is 19 M^(-1)s^(-1) at 222 K and 78 M^(-1)s^(-1) at 451 K? k = Ae^(-E_a/RT) ln(k_1/k_2) = -E_a/R * (1/T_2 - 1/T_1) E_a = R * ln(k_1/k_2) / (1/T_2 - 1/T_1) E_a = 8.3145 * ln(19/78) / (1/451 - 1/222) E_a = 8.3145 * ln(.24359) / (0.0022173 - 0.0045045) E_a = 8.3145 * -1.4122 / -0.0022872 E_a = 5133.7 J/mol
How do I find activation energy from a graph?
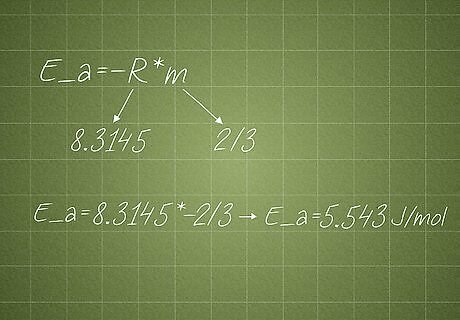
Find the slope and use the formula E_a = -R * m. Activation energy produces a straight line on a graph with ln(k) on the y (vertical) axis and 1/T on the x (horizontal) axis. Another rearranging of the Arrhenius equation (with m representing the slope of the line) gives you -E_a / R = m and thus E_a = -R * m. Here’s a quick rundown of the process: Calculate the slope (m) using the slope equation m = (y_2 - y_1) / (x_2 - x_1). To do this calculation, find the y and x coordinates at two separate points along the line. Plug the slope into E_a = -R * m, with R representing the ideal gas constant (8.3145). So, in a simple example, let’s say m = -2/3: E_a = -8.3145 * -2/3 → E_a = 5.543 J/mol



















Comments
0 comment